L’intelligenza di AlphaGo

Ricordatevi del 15 marzo 2016: quando una qualche versione del test di Turing sancirà l’indistinguibilità tra umani e software, lo scorso martedì sarà in ogni lista di pietre miliari dell’intelligenza artificiale. Questa è la data in cui per la prima volta uno dei migliori giocatori di go, Lee Sedol, è stato battuto da un software, e il suo nome è AlphaGo.

D’accordo, forse sto esagerando. Ma il confronto con la prima vittoria di un software contro un campione del mondo di scacchi 19 anni fa, è impietoso: la vittoria di AlphaGo è decisamente più importante di quella di Deep Blue su Kasparov. Non solo go è un gioco molto più complesso degli scacchi, e non solo la vittoria è arrivata all’improvviso, quando qualsiasi esperto stimava ancora almeno 5-10 anni di dominio umano; l’importanza viene dal principio di funzionamento di AlphaGo, incredibilmente più affascinante e scientificamente rilevante di quello di Deep Blue.

Alla fine di questo post spero di convincervi che l’entusiasmo è ampiamente motivato.

Software che giocano

Come fa un software tradizionale a scegliere la prossima mossa, a scacchi, dama, o semplicemente a tris? Tradizionalmente, in modo molto semplice: provando tutte le possibili combinazioni di mosse, cercandone una che porta alla vittoria, indipendentemente dalle risposte dell’avversario.

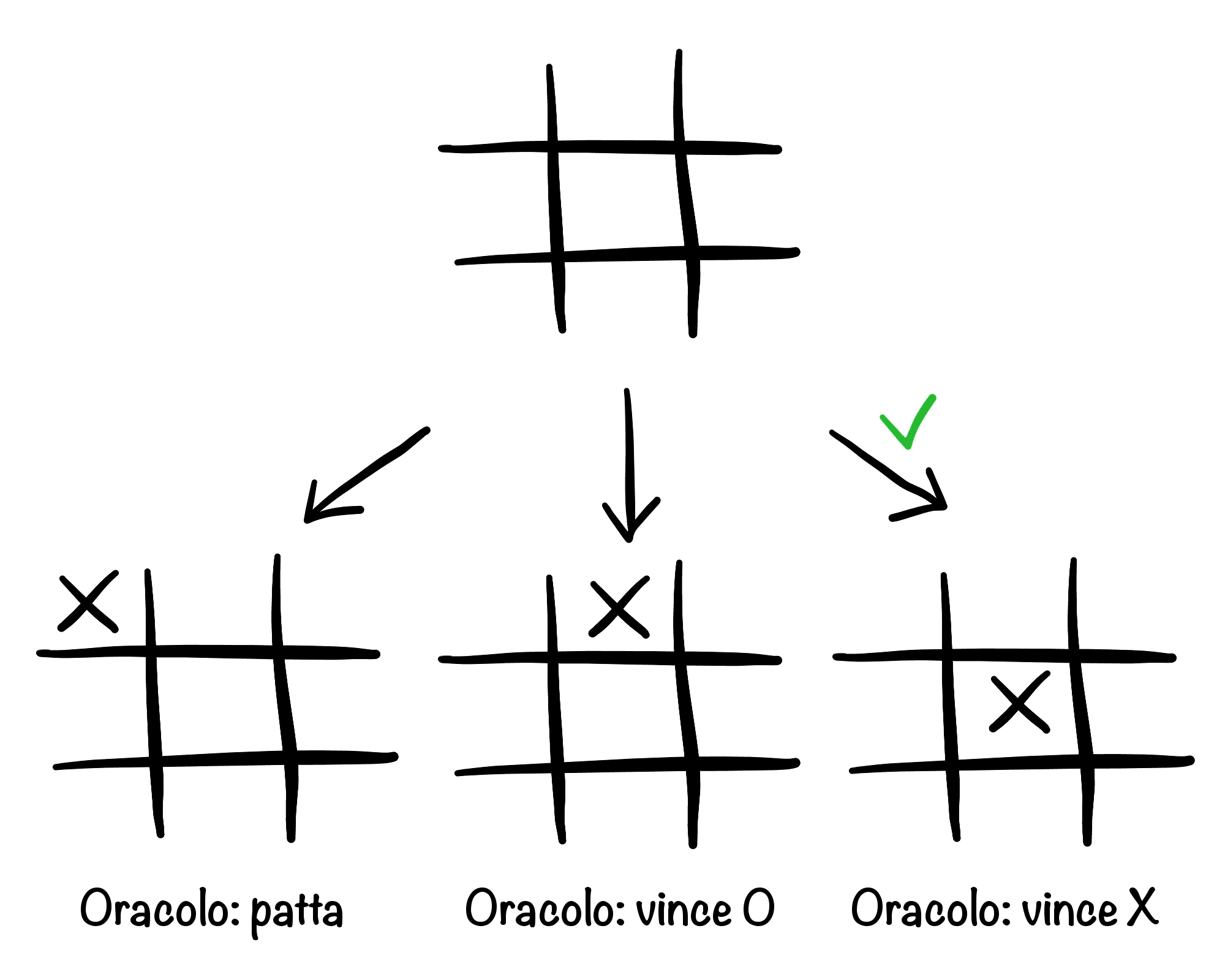
Avendo un oracolo, la prima mossa è semplice: basta scegliere quella che massimizza il risultato. In realtà tutte le posizioni sarebbero patte, ma se seguissimo la realtà non sarebbe un esempio interessante.

Per semplicità, pensiamo di dover fare la prima mossa a tris. Se avessimo un “oracolo” O1 che sa chi vincerà partendo da una qualsiasi posizione con una X, mi basterà provare ogni mossa e chiedere a O1 chi vince, e alla fine scegliere una qualsiasi di quelle vincenti, se esiste (spoiler alert: non esiste, sono tutte patte).

Ma questo sta solo spostando il problema: dato che O1 non esiste nella realtà, come faccio a sapere chi vince nelle posizioni con una X? È semplice, se assumiamo di avere un oracolo O2 che ci dice chi vince per tutte le posizioni che contengono una X e una O! Per ogni possibile mossa di X, chiediamo a O2 chi vince dopo ogni possibile risposta di O. Se ce n’è almeno una di queste che fa vincere O, possiamo assumere che la userà, refutando così la scelta iniziale di X; se invece non ci sono mosse vincenti per O, ma ce n’è almeno una che lo fa pattare, allora la mossa iniziale è patta; se tutte le mosse di O sono perdenti, allora la posizione iniziale è vinta per X.

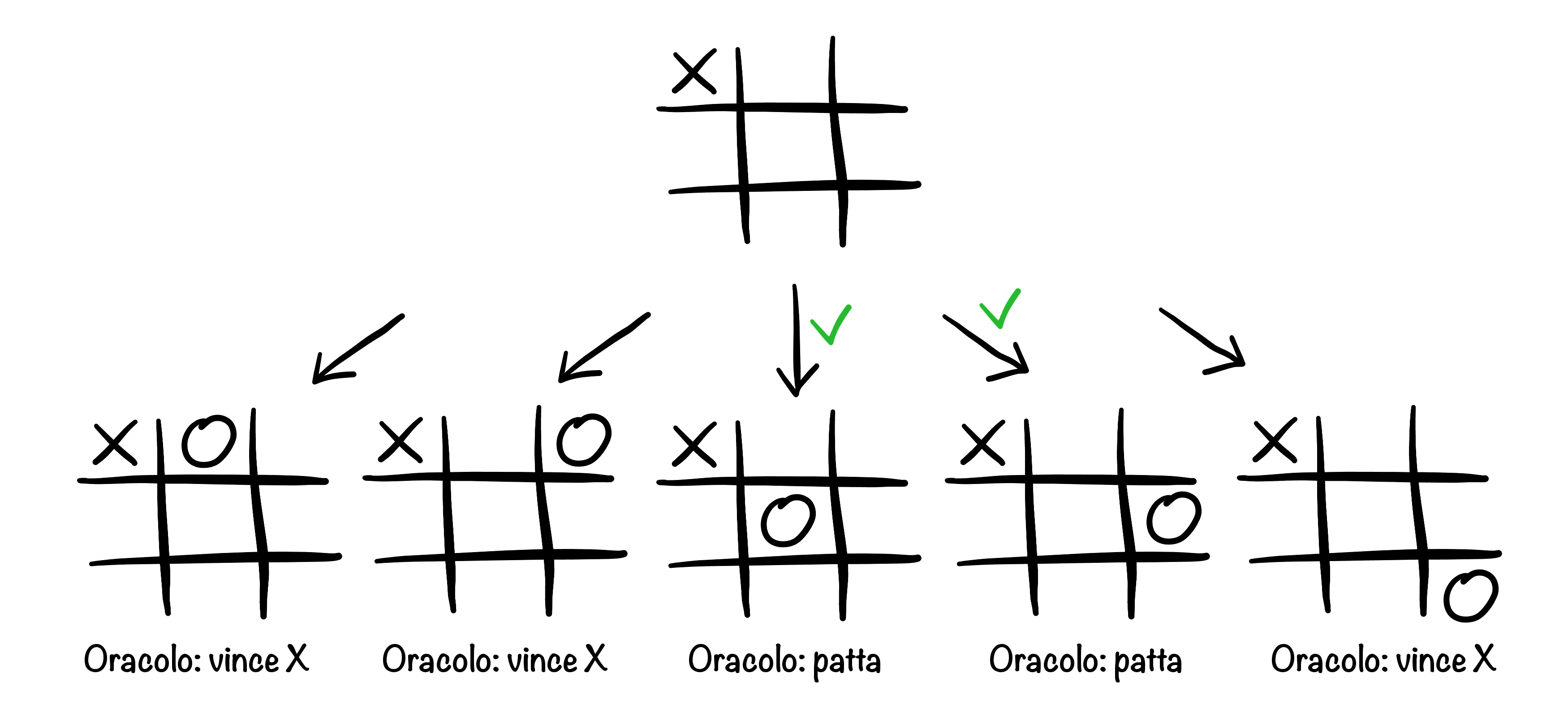
Come O1 fa a sapere che la partita è patta dopo che X gioca nell’angolo. Affidandosi a O2, deve assumere che O giochi in una posizione che massimizzi il suo risultato (e conseguentemente minimizzi il risultato di X). In questo caso, ancora con risultati inventati, O non può vincere ma può pattare.

Se continuiamo con questa strategia, usando O3 invece di O2 e così via, a un certo punto arriviamo a posizioni per cui non ci serve un oracolo, perché hanno già un tris per X o per O. Partendo da queste e risalendo alla prima mossa, possiamo finalmente valutare le nostre opzioni e decidere dove giocare.

Questo algoritmo si chiama minmax; il motivo di questo nome è che se assegniamo un valore numerico a ogni risultato, 1 per la vittoria di X, -1 per la vittoria di O, l’algoritmo alterna un passo di massimizzazione, quando muove X, a uno di minimizzazione, quando muove O: sia X che O cercano infatti la mossa migliore per sè, che nel caso di X è quella con il valore più alto, nel caso di O quella con il valore più basso.

Il problema è che il numero di posizioni da esplorare in questo “albero di ricerca” è di solito proibitivamente alto, aumentando esponenzialmente con il numero di livelli in cui l’algoritmo scende. Per limitare la ricerca a un numero gestibile di posizioni, dobbiamo “tagliare” (cioè, evitare di esplorare) alcuni rami. Per esempio, quelli per studiare mosse diverse dopo che abbiamo già attestato che una è vincente. Per questo motivo è conveniente cominciare la ricerca dalle mosse più promettenti, per aumentare la probabilità di poter tagliare rami importanti.

Ma anche questo non è abbastanza, e a un certo punto non si può fare altro che alzare bandiera bianca e sostituire i rami più profondi con una stima di ciò che direbbe l’oracolo in quella posizione. Negli scacchi, il bilancio materiale è l’ingrediente più importante di questa stima, ma sicuramente non l’unico: posizione del re, movimenti possibili, coordinazione, vicinanza dei pedoni alla promozione, e centinaia di altri segnali entrano nella valutazione euristica di una posizione. Il risultato sarà non più una decisa risposta “1” o “-1”, ma una misura della fiducia nella vittoria. Per esempio, se il nero ha catturato la regina bianca senza apparente compensazione, la valutazione potrebbe essere -0.9, a segnalare una posizione molto vicina alla vittoria per il nero.

Deep Blue, nella sua partita vincente contro Kasparov, seguiva esattamente questo algoritmo, e pure con una stima abbastanza rozza se confrontata con quelle dei programmi di scacchi attuali. La sua vittoria testimonia la capacità di IBM di costruire dei computer potenti, ma purtroppo è sempre molto più facile trovare problemi più complessi che non costruire l’hardware in grado di gestirli.

Go

Al contrario degli scacchi, principalmente un gioco di cattura di pezzi, go è un gioco di conquista di territorio: i giocatori si alternano nel piazzare pietre sul goban, una scacchiera 19×19, cercando di appropriarsi di territorio accerchiandolo con gruppi di pietre. Ogni gruppo (un insieme di pietre connesse orizzontalmente o verticalmente) che delimita un territorio deve essere “vivo”, cioè l’avversario non deve essere in grado di accerchiarlo completamente. Se questo succede, le pietre sono rimosse dal goban, ma spesso non si arriva alla cattura perché per un giocatore è più conveniente lasciare il gruppo avversario “virtualmente morto” e usare le mosse per qualcosa di più utile che completare l’accerchiamento.

Da un lato un gioco più semplice degli scacchi: molte meno regole, le pedine sono tutte uguali e una volta in gioco non si muovono. Ma è molto più complesso in almeno due direzioni.

1. La complessità emergente: secondo un detto comune, gli scacchi sono una battaglia e go è la guerra; guardando i professionisti spaziare da un lato all’altro del goban, la sensazione è esattamente quella. In ogni sezione del goban si gioca una battaglia locale, ma il cui risultato influenza le zone vicine; nel livello superiore, il giocatore deve decidere quale battaglia far avanzare con la prossima mossa: ogni pietra è un compromesso tra il guadagnare influenza e territorio in una parte del goban e perderlo in un’altra.

2. La complessità dell’albero di ricerca: negli scacchi il numero medio di mosse possibili per posizione è circa venti, e una partita media dura quaranta mosse; in go entrambi questi valori sono un ordine di grandezza più alto. Tradotto in dimensioni dell’albero di ricerca, significa un albero di ricerca di centinaia di ordini di grandezza più grande.

Per un programma, queste sono entrambe brutte notizie: la dimensione dell’albero significa che la porzione esplorabile è molto piccola, e lo spaziare da un lato all’altro del goban significa che non è possibile limitare la ricerca alle mosse vicine a quelle recenti.

Ma le cattive notizie non vengono mai da sole: finalizzare un territorio di solito può far guadagnare pochi punti, mentre giocare in una zona sgombra ne può far vincere o perdere decine. Di conseguenza, calcolare un “punteggio parziale”, come poteva essere il bilancio di materiale negli scacchi, è molto difficile, perché i territori tendono a non definirsi completamente fino a quasi la fine della partita.

Insomma, capire chi sta vincendo in una posizione è estremamente difficile (questo vale per gli esseri umani come per i programmi), e se la partita è equilibrata non ci sono indizi ovvi che possiamo usare per approssimare un oracolo.

Infatti, i primi programmi per go che cercavano di usare questi metodi non hanno mai superato il livello dei principianti. La prima rivoluzione è avvenuta quando è stata introdotta la cosiddetta “ricerca Montecarlo” – dove Montecarlo è un termine tecnico che significa “facciamo mosse a caso e vediamo che succede”. In pratica, per valutare una posizione un programma continua la partita in tanti modi diversi estraendo casualmente delle mosse, e il risultato è la frazione di partite vinte dal primo giocatore.

Questi programmi hanno raggiunto il livello di dilettanti mediamente forti, e non hanno mai battuto professionisti senza handicap (che nel go viene implementato permettendo al giocatore di posare un certo numero di pietre aggiuntive all’inizio della partita).

Detour: mi piacerebbe poter quantificare la forza di questi programmi con dei numeri, ma purtroppo il sistema di rating in go ha tutti gli svantaggi dovuti all’essersi sviluppato organicamente e in più di un posto. Approssimativamente, dai meno ai più forti, ci sono tre categorie: i principianti, da 30 kyu a 1 kyu; i dilettanti, da 1 dan a 9 dan; i professionisti, i cui gradi sono regolati da associazioni e vanno nuovamente da 1 dan a 9 dan. Giocatori con lo stesso grado di nazioni diverse non necessariamente hanno lo stesso livello. I migliori programmi con metodo Montecarlo raggiungono i 5-6 dan dilettanti; quelli senza, attorno ai 5 kyu.

Entrano le reti neurali

Le reti neurali sono uno dei metodi per costruire intelligenze artificiali attualmente più di moda, ma storicamente più controversi. Sembrano essere la chiave per risolvere moltissimi problemi su cui altri metodi non hanno avuto successo; hanno già dimostrato la loro utilità nel riconoscimento di immagini, nella loro descrizione in linguaggio naturale, nel riconoscimento vocale, nella traduzione automatica. Ma dalla loro introduzione, la ricerca si è interrotta diverse volte a causa di ostacoli che sembravano insormontabili, e che a volte sono stati superati con nuove architetture e teorie, altre semplicemente con il miglioramento dell’hardware.

Idealmente, una rete neurale mima il funzionamento di un cervello. Per quanto affascinante, questa affermazione è solo un’analogia, e ha una qualche giustificazione tecnica solo ad alto livello. Una rete neurale è infatti una collezione di neuroni che si parlano tra loro; ogni neurone prende i dati prodotti da molti altri e li combina in un modo relativamente semplice. La potenza della rete viene dall’avere un alto numero di neuroni che lavorano insieme.

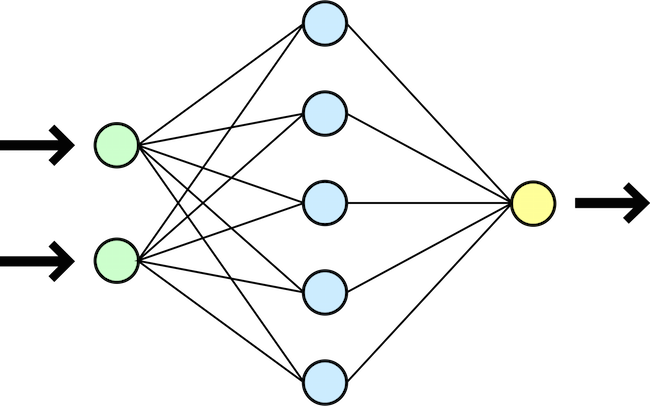
Una semplice rete neurale su tre strati (inclusi quelli di input e output), con 2 input e un output.

Matematicamente, l’obiettivo di una rete neurale è quello di approssimare una funzione non nota, ma di cui si conoscono degli esempi. Gli input vengono passati al primo strato di neuroni, che li inoltrano a tutti i neuroni del secondo strato attraverso collegamenti con un certo peso. I neuroni del secondo strato combinano tutti i loro input e emettono un output verso ogni neurone del terzo strato, ancora con un certo peso, e così via fino all’output finale. La rete “impara” adattando i pesi dei collegamenti dopo aver visto un esempio, cercando di avvicinare il suo risultato a quello atteso.

Il primo risultato teorico necessario è che le reti neurali possano fisicamente approssimare una funzione arbitraria. Questo è stato dimostrato negli anni novanta, a patto che la rete abbia almeno tre strati.

Nonostante questo, molti dei risultati recenti sono ottenuti con architetture composte da molti più strati (le reti in AlphaGo usano una quindicina di strati), chiamate deep learning. L’idea è che i neuroni degli strati più vicini agli input saranno stimolati da segnali semplici (per esempio, linee in una certa direzione), che negli strati successivi saranno amalgamati per creare neuroni stimolati da segnali più complessi (una parte del goban conquistata da un giocatore, per esempio).

Un esempio di segnali (features) che stimolano neuroni in strati diversi di una rete neurale per il riconoscimento facciale: quelli vicini agli input riconoscono segnali semplici, contrasti lineari o radiali; man mano che si prosegue, i segnali sono combinati e i neuroni riconosco occhi, bocche, e infine visi completi.
Autore: Mike Wang.

Per quanto la visione sia chiara, nella pratica aggiungere strati non è gratis: il tempo di esecuzione aumenta, ma soprattutto l’allenamento a partire dagli esempi diventa più complesso: l’effetto di una correzione sui pesi di uno strato si indebolisce con la distanza dallo strato di output, e di conseguenza più è profonda la rete e più è lento l’allenamento dei pesi al primo strato. Riuscire ad allenare reti di queste dimensioni è un successo recente, dovuto sia al miglioramento dell’hardware e dell’infrastruttura (distribuita su molti computer) sia a innovazioni teoriche e nuove tecniche di allenamento.

Parlando di nuove modalità di allenamento, una di queste è il reinforcement learning. Tradizionalmente, una rete neurale usa il supervised learning, che abbiamo assunto in precedenza: gli esempi sono costituiti da un input e dall’output atteso; la rete neurale viene eseguita sul primo e viene modificata per avvicinarsi al secondo. Ma spesso questi esempi non sono disponibili, e la rete neurale deve imparare da situazioni “reali”, dove la bontà o meno di un risultato su un certo input si scopre solo molto più avanti. Per esempio, se una rete neurale decide di piazzare una pietra in un certo posto, saprà solo alla fine della partita se è stata una buona idea.

AlphaGo

AlphaGo è stato sviluppato da DeepMind (una compagnia sorella di Google) negli ultimi due anni, anche se è stato annunciato pubblicamente solo lo scorso gennaio. In questi due anni, ha raggiunto e probabilmente superato gli esseri umani: nell’ottobre 2015 ha battuto 5-0 il campione europeo Fan Hui (2 dan professionista), e lo scorso martedì per 4-1 Lee Sedol, uno dei migliori giocatori degli ultimi 10 anni, ovviamente 9 dan professionista, il titolo più alto.

Sebbene l’effettiva superiorità in questo momento sia ancora opinabile (ci potrebbero essere “buchi” nella preparazione di AlphaGo che un umano potrebbe sfruttare dopo aver studiato più sue partite), la traiettoria è chiara, ed è chiaro che in pochi mesi AlphaGo sarà imbattibile.

Il funzionamento di AlphaGo è complesso, e unisce tecniche Montecarlo con reti neurali tradizionali, e la specialità di DeepMind, il reinforcement learning.

I dati iniziali sono circa centomila partite di dilettanti, giocate su un server online. Il primo passo è allenare una rete neurale S (per supervised) a predire le mosse degli umani. Poiché abbiamo un input (la posizione sul goban) e un output atteso (la mossa giocata dall’essere umano), si tratta di supervised learning. Non è la prima volta che viene provato, ma DeepMind ha aumentato la precisione dal 44% del miglior risultato precedente al 57%, e ha anche mostrato come piccole differenze nella precisione hanno un effetto enorme sulle capacità del programma finale.

Ma giocare in modo simile a dei dilettanti umani non è lo scopo di AlphaGo. Il secondo passo è costruire una seconda rete R (per reinforcement) a partire da S, migliorando le mosse prodotte con l’obiettivo di vincere la partita. La rete gioca milioni di partite, e per ognuna di queste la “ricompensa” arriva solo alla fine, ma è usata per incentivare (nel caso di vittoria) o disincentivare tutte le mosse prodotte durante la partita.

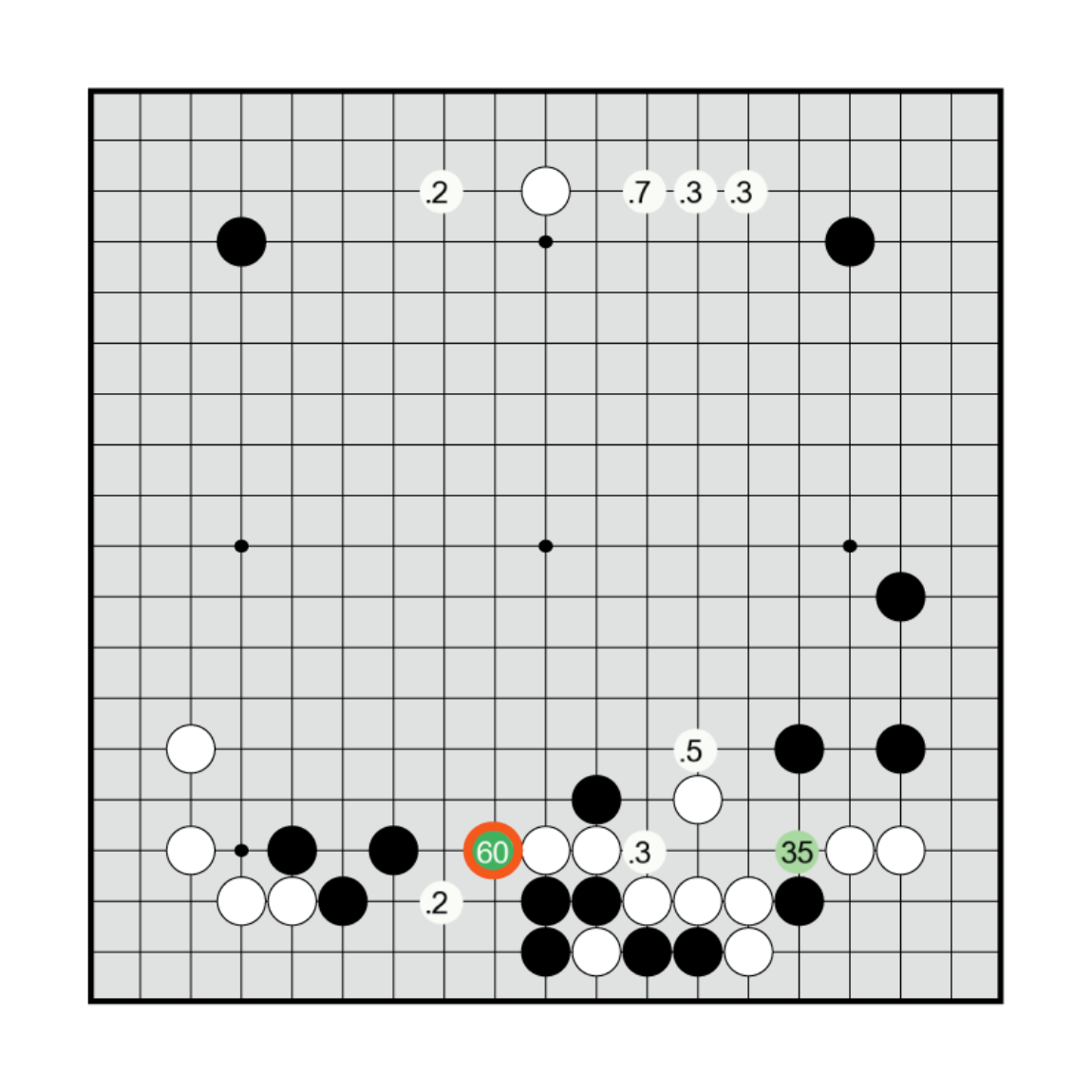
L’output di R in una posizione è una percentuale per ogni mossa che indica quanto AlphaGo pensa sia promettente. In questa posizione R pensa che ci siano solo due mosse molto promettenti, con il 60% e il 35%. Le caselle non indicate hanno valori minori di 0.1%.

Sia R che S possono già giocare a go, dato che il loro output è la prossima mossa. Dai test di DeepMind, R batte S nell’80% delle partite, ma soprattutto batte un altro programma con rating 2 dan nell’85% dei casi, senza alcun tipo di ricerca (cioè, rispondendo immediatamente).

Ma AlphaGo usa la ricerca, per quanto poco (Deep Blue esaminava un numero di posizioni migliaia di volte maggiore, per un albero di ricerca molto più piccolo) – non usarla significherebbe non sfruttare il fatto che durante la partita la posizione attuale è nota e può essere quindi usata per integrare l’architettura della rete neurale. Di conseguenza, abbiamo bisogno di una stima dell’oracolo.

L’output di V dopo aver piazzato una pietra in ogni casella a partire dalla posizione mostrata in precedenza (sono mostrate solo le mosse con valori maggiori o uguali a 50). La mossa migliore per V è una delle due isolate da R; l’altra invece non è tra le migliori per V.

Come ricordate, valutare una posizione a go è particolarmente difficile, perché non esistono semplici euristiche per estrarre informazioni dalla posizione. Il terzo passo quindi è allenare una terza rete neurale V per valutare una posizione, a partire da circa 30 milioni di posizioni di partite giocate da R contro sè stessa. È essenziale non usare tutte le posizioni di una partita; uno dei possibili problemi nell’apprendimento automatico è che il sistema non identifichi i caratteri salienti degli esempi in modo da poter usare ciò che ha imparato anche in condizioni nuove, ma che al contrario “memorizzi” gli esempi. Le posizioni di una partita sono ampiamente correlate in go, e usarle tutte per l’allenamento porterebbe esattamente a questo risultato: la rete imparerebbe che una certa posizione usata per l’allenamento ha una certa valutazione, ma si perderebbe nel valutare una posizione mai vista.

Il quarto passo è la ricerca, in realtà abbastanza simile a quella di altri programmi, ma con due differenze:

1. l’albero viene esplorato dando priorità alle mosse che S considera probabili (curiosamente, usare la più forte R dà risultati peggiori, probabilmente perché le sue proposte sono più concentrate in poche mosse, mentre S è più sparsa);

2. al momento di fermare la discesa, la valutazione è la media di quelle di V e del metodo Montecarlo (usando come probabilità per le mosse quelle ottenute da una versione rapida ma meno accurata di S).

È interessante confrontare i risultati ottenuti usando solo il metodo Montecarlo, solo V, o entrambe: individualmente, Montecarlo rende AlphaGo quasi un 9 dan dilettante, più forte che usando solo V (7 dan dilettante); ma insieme, hanno permesso di battere Fan Hui con una performance da 3 dan professionista (tutti i risultati sono per la versione di ottobre, significativamente più debole di quella che ha battuto Lee Sedol).

Conclusioni

Fino a questo momento spero di avervi convinto dell’importanza di AlphaGo nel mondo del go e di quanto sia impressionante sia da un punto di vista di risultati che tecnico. Ma tutto ciò non dà ancora la visione di un roseo futuro in cui i problemi dell’umanità saranno risolti da macchine superumanamente intelligenti (se non addirittura coscienti!).

La filosofia di DeepMind, che tra le altre cose sta cominciando a collaborare con il sistema sanitario inglese, non è quella di creare intelligenze artificiali adatte a risolvere un problema specifico, come può essere quello del riconoscimento vocale. Al contrario, la speranza è di inventare delle tecniche che possono essere usate in generalità per risolvere molti problemi diversi.

Per esempio, uno dei loro primi successi è una rete neurale per giocare a molti videogiochi degli anni ottanta, il cui unico input è la serie di frame generati dal videogioco, oltre al punteggio attuale; in particolare, la rete può decidere di premere dei pulsanti, ma deve scoprire il loro effetto da sola. L’architettura della rete non cambia da gioco a gioco, né il metodo di allenamento, eppure la rete riesce a imparare giochi anche molto diversi tra loro.

Nel suo complesso, AlphaGo è chiaramente un programma molto specializzato. Ma le tre reti neurali S, R, V non lo sono, nella loro architettura come nei metodi di apprendimento. Se nei circoli di go si è impressionati dalla performance del programma completo, i veri risultati significativi per l’intelligenza artificiale sono da un lato la capacità di allenare R, nonostante l’esito di una mossa diventi noto centinaia di mosse più tardi, e dall’altro l’effetto pubblicitario di un ulteriore problema che ha ricevuto un miglioramento rivoluzionario grazie all’apprendimento artificiale.

Insomma, ancora non aspettiamo col fiato sospeso la soluzione al riscaldamento globale, ma possiamo essere un po’ più ottimisti.