Problemini per Ferragosto 2022

Anche questa volta i problemi sono tratti dal libro di Tadao Kitazawa Arithmetical, Geometrical and Combinatorial Puzzles from Japan. I primi due sono sicuramente estivi, gli altri forse un po’ di meno: ma non sono richieste conoscenze matematiche. Le risposte, come al solito, tra una settimana.

1. Quadrati latini
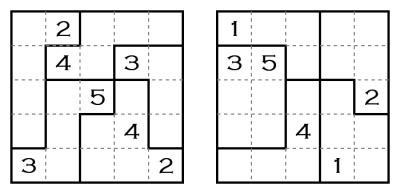
Da quando i sudoku sono di moda, tutti sanno cos’è un quadrato latino: un quadrato di n×n caselle dove in ogni riga e in ogni colonna ci sono i numeri da 1 a n. Anche i due quadrati qui sotto sono latini, ma c’è un trucco: in ciascuna delle aree in cui sono divisi i quadrati i numeri che trovate scritti sono ripetuti un’altra volta, mentre gli altri numeri appaiono una volta sola nell’area. Riuscite a ricostruire i quadrati?

2. Quadrati a torre
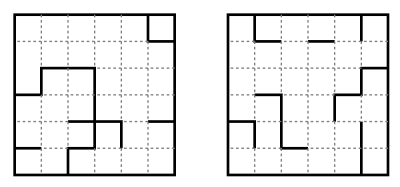
Un quadrato a torre è un quadrato il cui lato è un numero triangolare n (1, 3, 6, 10, …), dove in ogni riga e ogni colonna si trova un’occorrenza di 1, due occorrenze di 2, tre occorrenze di 3, e così via. Nei due schemi qui sotto trovate due quadrati a torre di lato 6, e quindi con i numeri da 1 a 3. Dove c’è una sbarretta continua di divisione tra due quadratini, i numeri ai due lati sono identici (e quindi non può mai esserci un 1…), mentre se non c’è i due numeri sono distinti. Anche qua, riuscite a ricostruire i quadrati?

3. Manca qualcosa
Ciascuna delle sedici carte triangolari che vedete qui sotto contiene tre numeri da 1 a 9. Greta dà una rapida occhiata alle carte ed esclama: “Sono sicura che non è possibile prenderne tre in modo da avere tutti i numeri da 1 a 9!” Come fa a esserne certa?

4. Sposta e incrementa
Avete cinque carte numerate da 1 a 5 e messe in fila ordinata, come in figura. A ogni mossa potete prendere una carta e metterla tra altre due: a quella carta non succede nulla, ma le due carte vicine aumentano di 1 il loro valore. Qual è il numero minore di mosse per fare sì che tutte le carte abbiano lo stesso numero?

5. Calcolo… spezzato
Ricostruite il puzzle componendo tutte le addizioni e sottrazioni (gli uguali sono sempre nella penultima colonna). Attenzione! Per complicare la vita, ci sono quattro tessere di troppo…