Risposte ai problemini per Pasqua 2022
Se non siete riusciti a risolvere i problemi della scorsa settimana, finalmente ci sono le soluzioni!
Attenzione alle tossine
Non possiamo riconoscere il tipo di pastiglie, ma possiamo vedere che sono diverse. Prendendo una pastiglia per tipo assumiamo 47 tossine; quindi possiamo prenderne tre per tipo e assumeremo 141 tossine. Abbiamo ancora la possibilità di assumere 38 tossine: con due pastiglie da scatole diverse siamo certi di non superare quel valore. In definitiva dunque possiamo prendere 11 pastiglie, tre da una confezione qualunque e quattro da ciascuna delle altre due.
Uno vale tutti gli altri
La somma dei numeri a 1 a 12 è 78; pertanto la somma dei numeri maggiori di ciascun insieme è 39. Il numero di insiemi possibile deve essere maggiore di 3, perché con tre insiemi la somma dei numeri maggiori è al più 33; ma poiché ogni insieme deve avere almeno tre elementi abbiamo che ci sono esattamente quattro insiemi. A questo punto è abbastanza semplice trovare la partizione adatta: per esempio, {12,9,3}, {11,7,4}, {10,8,2} e {6,5,1}.
<!– Non solo non è semplice generalizzare il risultato all’insieme dei primi n naturali, ma spesso non è nemmeno possibile: per esempio se i numeri fossero 14 la loro somma è 105 che è dispari, quindi non esiste una partizione simile. –>
Uno oppure dieci
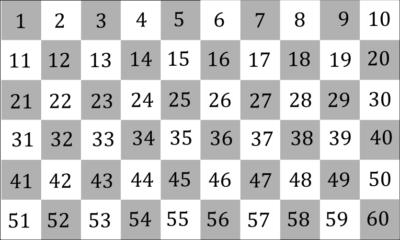
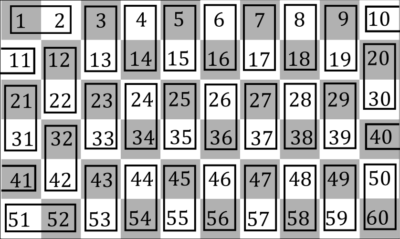
Disponete i numeri da 1 a 60 ordinatamente in una scacchiera 6×10 come mostrato in figura qui sopra. È immediato che se i due numeri differiscono tra di loro di 10 unità saranno su caselle di colore diverso; lo stesso capita se i due numeri differiscono tra l’oro di un’unità, salvo nel caso in cui il primo numero termina per 0 e il secondo per 1. Poiché la coppia (10, 11) usa due caselle bianche, occorre che ci sia una coppia che usi due caselle nere. Poiché però 20 e 30 sono già stati usati, l’unica possibilità è che 40 e 41 siano accoppiati, e quindi il numero che fa coppia con 41 è 40. Resta da dimostrare che in effetti si possano creare le coppie: nella figura qui sotto è mostrata una possibile ripartizione.
Baci e abbracci
Per simmetria possiamo immaginare che le ragazze siano almeno quanto i ragazzi. Visto che tutto abbracciano almeno due persone, i casi possibili sono avere quattro ragazze e due ragazzi oppure tre ragazze e tre ragazzi. Nel primo caso però i due ragazzi devono avere abbracciato tre ragazze per un totale di sei abbracci, mentre le quattro ragazze hanno ciascuna abbracciato due ragazzi per un totale di otto abbracci, il che è assurdo. Pertanto ci sono tre ragazze e tre ragazzi. Consideriamo ora le due persone che ne hanno abbracciate altre tre; se fossero entrambe dello stesso sesso, ciascuna di loro avrebbe abbracciato tre persone dell’altro sesso. Ma la terza persona del sesso delle prime due non avrebbe potuto abbracciare nessuno, il che non è ammesso. Pertanto le due persone che ne hanno abbracciate tre sono di sesso diverso, e visto che ciascuna di esse non può abbracciare più di due delle altre persone, si devono abbracciare tra loro.
Per completare la risposta, occorre verificare che effettivamente si possa trovare una configurazione di abbracci. Se le ragazze sono A,B,C e i ragazzi sono X,Y,Z, una possibile configurazione è data dagli abbracci (A,X), (A,Y), (A,Z), (B,X), (B,Y), (C,X), (C,Z). A e X hanno abbracciato tre persone, mentre B, C, Y e Z ne hanno abbracciate due.
Furto di crostate
Poiché il numero di crostate è primo, nessuno dei due Fanti neri può essere stato il primo a entrare in cu cina; e poiché ne rubano solo una parte, non possono essere nemmeno stati l’ultimo. Supponiamo che il primo a entrare sia stato il Fante di Quadri: ha lasciato un numero dispari di crostate, che quindi deve essere stato un multiplo di tre. Non può essere 3 (il Fante di Picche ne lascerebbe una, e devono ancora entrare due Fanti) e nemmeno 9 (il Fante di Picche ne lascerebbe tre, e il fante di Fiori non potrebbe rubarne nessuna). Pertanto il primo a entrare è stato il Fante di Cuori, che ha lasciato un numero di crostate multiplo di 3 o di 4.
Se il Fante di Cuori avesse rubato 9 crostate, ne sarebbero rimaste 4; il Fante di Fiori ne avrebbe rubata una, il Fante di Picche due e ne sarebbe rimasta una per il Fante di Quadri, impossibile. Se il Fante di Cuori ne avesse rubato 7, ne sarebbero rimaste 6; il Fante di Picche ne avrebbe rubato 4 lasciandone due, impossibile. Se il Fante di Cuori avesse rubato una sola crostata, ne rimarrebbero 12. Se il secondo fosse stato il Fante di Fiori, ne avrebbe preso 3; il Fante di Picche ne avrebbe preso 6 lasciandone 3 per il Fante di Quadri, impossibile. Se invece il secondo fosse stato il Fante di Picche, ne avrebbe prese 8 lasciandone 4 per il Fante di Fiori, impossibile. Se infine il Fante di Cuori ne avesse rubato 5, ne sarebbero rimaste 8; il Fante di Fiori ne avrebbe rubate 2 lasciandone 6, il Fante di Picche ne avrebbe rubate 4 lasciandone 2, che sarebbero state rubate dal fante di Quadri. Questa è dunque l’unica soluzione possibile, ed è stato il Fante di Cuori ad aver rubato più crostate.