Sorteggi e quote rosa
È di questi giorni la notizia che al liceo scientifico Talete di Roma, che ha avuto più richieste del numero di posti disponibili per la singola classe dell'”indirizzo matematico”, al posto di fare un test di ammissione o di usare voto di terza media si è scelto di sorteggiare gli ammessi… ma con le “quote rosa”, rispettando la proporzione di genere rispetto al numero di domande presentate. (Per la cronaca, il titolo è fuorviante: i posti non sono solo 10 ma 25). Che si può dire al riguardo?
Personalmente ritengo che usare i voti dell’anno precedente non sia un ottimo sistema, perché scuole diverse, e addirittura classi diverse all’interno della stessa scuola, possono avere criteri di valutazione diversi; avrei comunque fatto fare i test di ammissione, perché in fin dei conti stiamo parlando di 46 ragazzi – 31 maschi e 15 femmine – e li si sarebbe potuti lasciare sufficientemente distanti. So che ci sono voci discordanti sulla validità di questi test, ma andremmo fuori tema: qui il punto è “se sorteggio deve essere, lo si fa senza paletti per genere”?
Bene. Invece che parlare del nulla, mi sono messo a fare i conti. Dovete sapere che questo tipo di estrazione casuale è ben studiato in matematica e ha un nome specifico: distribuzione ipergeometrica. Il suo modello è prendere un’urna con un numero definito di palline bianche, nel nostro caso corrispondenti alle femmine, e nere – che corrispondono ai maschi – ed estrarne un certo numero, cioè i fortunati ammessi alla classe matematica. Se il numero totale di palline è n e le palline bianche sono h, la probabilità che quando se ne estraggono r quelle bianche siano k è data dalla formula qui sotto, dove le parentesi con due espressioni una sopra l’altra corrispondono alle combinazioni.
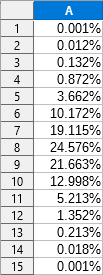
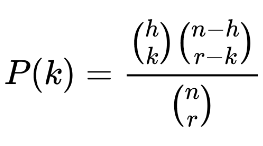Se vi siete spaventati dalla formula avete ragione. Quello che conta è che la formula esiste e quindi si può calcolare quant’è la probabilità che in un’estrazione di 25 studenti da un insieme di 46 il numero di femmine sia 0, 1, 2, … 15. Essendo io pigro e non fidandomi di come Excel sappia fare bene i conti con risultati parziali che possono essere molto alti, sono andato a cercarmi un sito apposito a cui far fare i conti. I risultati sono mostrati nella tabella in alto, dove non è indicata la probabilità di non sorteggiare nessuna ragazza, perché minore dello 0,001%. Con la segregazione per genere siamo certi che la classe avrà otto ragazze. Con il sorteggio totale, invece?
I conti sono presto fatti. La probabilità che ci siano esattamente 8 ragazze è un po’ meno di un quarto, ma questo non ci dice molto. Più interessante notare che la probabilità che ci siano più di otto ragazze (il 41,4%) è maggiore di quella che ce ne siano di meno (il 34,0%), ma anche questo era immaginabile a priori, perché avevamo arrotondato per difetto il numero di ragazze ammesse. Ma la parte che almeno per me è più interessante è un’altra. La probabilità che con un’estrazione casuale siano ammesse almeno 6 ragazze è dell’85,1%, e se scendiamo ad almeno 5 – con meno di così qualcuno potrebbe poi parlare di discriminazione – si arriva al 95,3%. Detto in altri termini, un sorteggio del tutto casuale avrebbe con ogni probabilità portato a risultati non molto distinguibili da quello pilotato che è stato previsto. E allora, mi chiedo, perché darsi tanta pena per farlo?
