Risposte ai problemini per Pasqua 2020
Siete rimasti bloccati con i problemini? Nema problema, solo soluzioni!
1. Moltiplicazioni in catena
Cominciamo a vedere che non possono esserci due cifre dispari consecutive nella lista. Se ci fossero, possiamo prendere le prime due che appaiono. Ma come possono essere state aggiunte alla lista? Se fossero il prodotto di due altre cifre precedenti, anch’esse devono essere dispari; se la prima fosse l’ultima cifra di un prodotto e la seconda la prima di un altro prodotto, comunque il primo prodotto dovrebbe essere di due cifre dispari. In ogni caso la nostra ipotesi di aver scelto la prima coppia di cifre dispari è errata.
Questo però significa che ogni cifra dispari che troviamo è la prima cifra di un prodotto; quindi il 9 non potrà mai esserci perché il prodotto di due numeri di una cifra è sempre inferiore a 90; il 7 non potrà mai esserci perché l’unico prodotto di due numeri di una cifra che cominci per 7 è 9·8=72 ma il 9 non si trova nella lista; il 5 non può esserci perché gli unici prodotti di due numeri di una cifra che comincino per 5 sono 6·9=54 e 7·8=56 e né 7 né 9 sono presenti; lo 0 non può esserci perché il primo zero nella lista deve essere il prodotto di un 5 per un numero pari, e non ci sono 5.
<!– Inutile dire che la successione si trova su OEIS. –>
2. Tocca non ripetersi
Innanzitutto, costruendo la lista si troveranno a un certo punto tre 8 consecutivi. Essi genereranno la successione 6, 4, 6, 4 che a sua volta genera 2, 4, 2, 4, 2, 4 che genera 8, 8, 8, 8, 8. Similmente i cinque 8 consecutivi ne generano 13, e in genere k 8 consecutivi ne generano 4*k−7. Poiché il numero di 8 consecutivi continua a crescere, la lista non può essere periodica.
3. Non proprio Fermat
Poiché è facile vedere che x ≠ y, possiamo supporre senza perdita di generalità che x < y < z. Spostando il termina yn al secondo membro e fattorizzando, abbiamo che xn = (z−y)(zn−1+yzn−2+…+yn−1) ≥ 1+nxn−1 > xn, che è assurdo.
4. Un numero irrazionale
Per la regola di Ruffini, una soluzione razionale di un’equazione polinomiale a coefficienti interi è della forma p/q, dove p è un fattore del termine noto e q un fattore del coefficiente del termine di grado più elevato. In questo caso questo coefficiente è 1, quindi le soluzioni razionali devono essere intere, il che è impossibile.
5. Distanziamento
Per la prima parte, supponiamo che esista un poligono ABC…MN. Possiamo supporre senza perdita di generalità che NA < AB. Ma allora dev’essere AB < BC, perché B non è il punto più vicino ad A. Similmente, BC < CD e così via, fino a MN < NA. Mettendo insieme tutta questa catena, abbiamo che AB < NA, il che contraddice l’ipotesi.
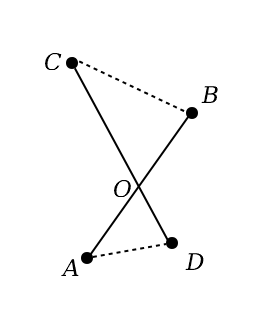
Per la seconda parte, supponiamo che come in figura il punto B sia il più vicino ad A, e il punto D sia il più vicino a C. Allora per definizione AD > AB e CB > CD. Ma allora AD + CB > AB + CD = AO + OB + CO + OD, il che è impossibile perché AD < AO + OD e BC < BO + OC.



