Risposte ai problemini per Ferragosto 2019
Come per Pasqua, anche stavolta ho preso i problemini da The Ultimate Mathematical Challenge: sono rispettivamente i numeri 170, 171, 172, 174 e 175.
1. Trapezio
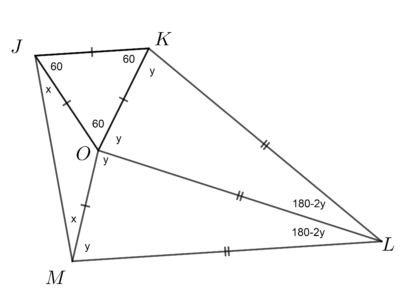
Il triangolo JOK è equilatero, quindi i suoi angoli sono di 60°. Il triangolo JOM è isoscele in O, quindi gli angoli JMO e OJM hanno lo stesso valore x. Similmente i triangoli KLO e OLM sono isosceli, quindi gli angoli LKO, LOK, LOM, LMO hanno lo stesso valore y, e pertanto gli angoli OLM e OLK valgono 180°−2y. A questo punto sappiamo che in un trapezio gli angoli relativi ai lati obliqui sono supplementari (la loro somma è 180°); dagli angoli JKL e KLM abbiamo che y=80°, e dagli angoli KJM e JML ricaviamo infine che JMO=20°.
2. Tre su quattro
Se sommate tutti e quattro i risultati, ogni numero sarà stato contato tre volte. Poiché la somma è 618, la somma dei quattro numeri iniziali è 206; sottraendo la minore delle quattro somme, cioè 115, ricaviamo che il numero maggiore è 91.
3. La tavola rotonda
Poiché nessuna ragazza è vicina a Walter, i suoi vicini sono Vincenzo e Zeno; inoltre Yolanda è vicina a Vincenzo, quindi l’ordine (ciclico) dei posti è VWZXY. Sempre dall’affermazione relativa a Vincenzo, sappiamo che Walter è di Domodossola. L’aostana deve pertanto essere Xenia, e quindi Yolanda è di Enna. Il cagliaritano non può essere Zeno, pertanto è Vincenzo, e Zeno deve essere di Belluno.
4. Non solo biciclette
Eliminiamo una ruota per ogni sella. Rimaniamo così con sei ruote per sette mezzi: i tricicli (che hanno perso una ruota nell’operazione) potrebbero essere uno oppure due, ma in quest’ultimo caso le biciclette sarebbero anch’esse due, cosa vietata dalle ipotesi. Pertanto c’è un triciclo e quattro biciclette, mentre i monocicli sono i due mezzi restanti.
5. Gara a quiz
Ci sarà un numero x di problemi risolti da entrambe le ragazze, che contano per cinque punti cadauno, e un numero 2×(60−x) di probemi risolti da una sola ragazza, che contano per quattro punti. Sapendo che il punteggio totale è 312 punti, si ottiene x=56.



