La dimostrazione matematica più lunga
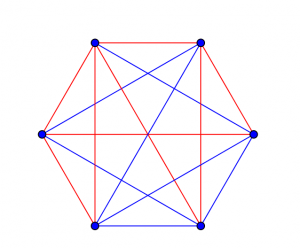
Uno dei campi più strani della matematica è la teoria di Ramsey. La sua stranezza non sta certo nella complessità dei suoi teoremi, che possono essere descritti anche a un ragazzino. Il teorema di Ramsey, per esempio, considera i grafi completi di grado n, cioè le configurazioni formate da n punti e da tutti i segmenti che uniscono una coppia qualunque di punti: potremmo insomma dire che abbiamo un n-gono con tutte le diagonali, ma dobbiamo ricordarci che lati e diagonali sono in questo contesto la stessa cosa. Il teorema afferma che se scegliamo un numero qualunque c di colori diversi per colorare i segmenti e un numero naturale k, allora esiste un numero N tale che il grafo completo di N punti conterrà sicuramente un sottografo completo di ordine k i cui segmenti sono di un solo colore. Il guaio è che le dimostrazioni nella teoria di Ramsey sono spesso molto complicate, perché il numero di elementi in gioco cresce più che esponenzialmente; per i risultati di esistenza e si riescono solo a fare stime grossolane. Tanto per dire, è facile dimostrare che se c=2 e k=3 allora il più piccolo N è 6: quindi se si disegna un esagono con tutte le sue diagonali e si colorano lati e diagonali in rosso oppure in blu siamo certi di avere un triangolo tutto rosso oppure tutto blu. Ma già se k=5 nessuno sa qual è il più piccolo valore di N, e per k=6 nessuno sa se sapremo mai la risposta. Roberto Zanasi lo racconta qui e qui.