Risposte ai quizzini di Ferragosto 2018
Anche stavolta i problemi arrivano dalla Olimpiada Matemática Española (anno 1994)
Successioni e quadrati
Basta dimostrare che dato un quadrato perfetto nella successione se ne può trovare un altro. Partiamo dunque da a²; se la ragione della successione è d, dopo 2a+d termini arriviamo a a²+2ad+d² che è (a+d)².
Meteorologia
Perché i giorni di sole siano il triplo di quelli di pioggia, la loro somma deve essere multipla di 4. La somma di tutti e sei i valori è 2018, che divisa per 4 dà resto 2; l’unica regione i cui giorni di sole e di pioggia diano resto 2 è F, che quindi è da eliminare.
Un triangolo particolare
Notate che gli angoli ABC e ACB misurano 72 gradi. Bisecate l’angolo in C, e sia D il punto in cui incontra il lato AB. Il triangolo BCD ha gli stessi angoli di ABC, quindi è simile ad esso; ma anche il triangolo ACD è isoscele, quindi CD=AD=a, e BD=b−a. Abbiamo pertanto che b/a=a/b−a, da cui b/a=(√5+1)/2.

Tre per sette
Nessuna colonna può avere tre pedine dello stesso colore, per esempio bianco: se così fosse, infatti, nessun’altra colonna potrebbe avere due pedine di quel colore, altrimenti si formerebbe un rettangolo: restano pertanto solo quattro possibilità diverse (NNB, NBN, BNN, NNN) e alla sesta colonna bisognerà ripeterne una di quelle quattro e avere un rettangolo. Ma ci sono comunque solo sei possibilità di scegliere tre pedine di colori diversi (NNB, NBN, BNN, NBB, BNB, BBN) e quindi la settima colonna dovrà ripetere una di quelle precedenti.
<!– Con sei colonne sarebbe invece possibile non avere rettangoli, si veda la figura qui sotto.
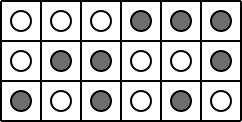
–>
Triangolazione
Se abbiamo ntriangoli, in tutto avremo 3n lati. Di questi, m sono esterni (quelli del poligono di partenza), mentre gli altri 3n−m sono interni e quindi contati due volte. Ma allora 3n−m deve essere pari, quindi m e n devono avere la stessa parità, e in definitiva m+n deve essere pari.
<!– Si può anche dimostrare – per induzione, ovvio… – che il numero v di vertici interni è uguale a (n−m+2)/2. –>



