Quizzini di Ferragosto 2018

Soliti problemini matematici abbastanza d’annata e direi non troppo complicati: la risposta sarà data tra una settimana.

Successioni e quadrati

In una successione aritmetica, la differenza d tra due elementi successivi è costante. È facile costruire una successione aritmetica di numeri positivi che non contenga alcun quadrato perfetto: prendiamo per esempio 7, 17, 27… Dimostrate che però se essa contiene un quadrato perfetto allora ne avrà infiniti.

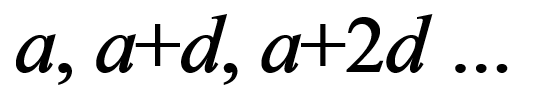
Meteorologia

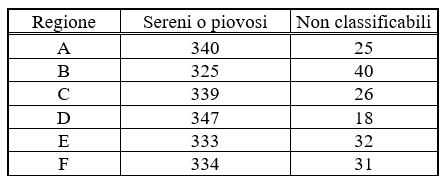
L’ente del turismo di Matelandia vuole compilare una statistica dei giorni di sole o pioggia nella nazione. Chiede i dati di sei regioni, solo che non si è ben spiegato e quindi i dati arrivano come “giorni di sole oppure pioggia”, come vedete nella tabella qui sotto. Recuperati i dati completi con la suddivisione ulteriore tra giorni di sole e di pioggia, ci si accorge che se si esclude una delle regioni allora il numero di giorni di sole è il triplo di quelli di pioggia. Quale regione è da escludere?

Un triangolo particolare

In un triangolo isoscele ABC l’angolo al vertice A misura 36 gradi. Calcolate il rapporto b/a tra i lati AC e BC.

Tre per sette

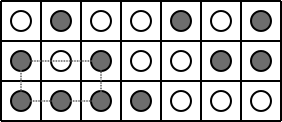
Si prendano ventun pedine, alcune bianche e altre nere, e le si dispongano in una scacchiera 3×7, una per casella. Si dimostri che ci sarà sempre un rettangolo (non banale, quindi non 1×k) ai cui vertici ci siano pedine dello stesso colore. Il rettangolo è con i lati paralleli alle caselle, per completezza.

Triangolazione

Dato un poligono convesso di m lati, lo si triangoli: si aggiunga cioè un certo numero di punti interni e lo si suddivida in n triangoli, tali che non ci sia nessuna sovrapposizione tra di essi e due triangoli possano avere un comune o un vertice o un lato (nessun vertice di un triangolo tocca un punto interno a un lato, insomma). Si dimostri che m+n è pari.