Problemini per Natale 2017

Quest’anno ho preso i quizzini da Gifted Mathematics che ha un piccolo problema: non ci sono le soluzioni. Quindi magari la mia soluzione è sbagliata… Thriller in più. Al solito, le soluzioni a San Silvestro. (Ah, i problemi dovrebbero essere in ordine decrescente di difficoltà)

1. Biglie e sacchetti
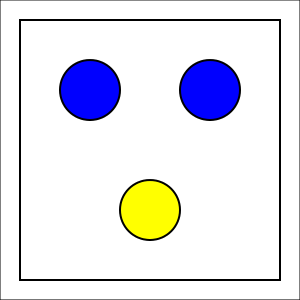
Alice e Marco stanno facendo un gioco. In una scatola ci sono sei biglie, identiche al tatto, tre blue e tre gialle; lì vicino ci sono due sacchetti non trasparenti. Alice benda Marco, mischia le biglie e gliele fa mettere due in un sacchetto e quattro nell’altro. Marco non può vedere nulla, ma può capire quale sacchetto ha due biglie e quale quattro. A questo punto Alice invita Marco a prendere due biglie sa un sacchetto a scelta; se saranno dello stesso colore avrà vinto, altrimenti avrà perso. A Marco conviene prendere le due biglie dal sacchetto che ne ha due, o sceglierne due dall’altro?

2. Tagliare una pizza
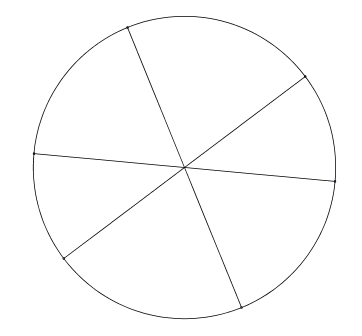
Prendete un cerchio e scegliete a caso tre diametri distinti, che lo divideranno in sei settori. Qual è la probabilità che due dei settori abbiano un’area almeno pari a un quarto del cerchio?

3. Una strana funzione
F è una funzione non decrescente definita per tutti gli x compresi tra 0 e 1, per cui valgono le seguenti proprietà:

(i) F(x/3) = F(x)/2,
(ii) F(1 − x) = 1 − F(x)

Calcolate F(1/42).

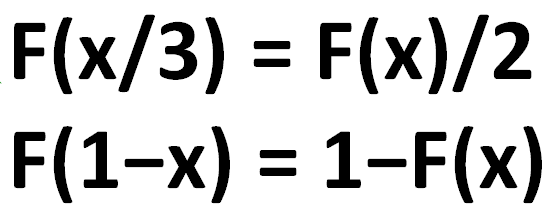
4. Somme e divisori

Trovate tutti gli interi n tali per cui la somma di n e del suo maggior divisore proprio sia 2013.

5. Numeri paladini
Chiamiamo un numero n “paladino” se il numero dei suoi divisori (positivi) è uguale al numero di cifre del numero stesso. Per esempio, 121 è un numero paladino, avendo come unici divisori 1, 11, 121. Trovate un numero paladino di quattro cifre e minore di 1300.