Moltiplicazione e commutatività

Ripensando al post precedente, dove mi chiedevo retoricamente se 3×5 fosse davvero uguale a 5×3, ho pensato che forse potrebbe essere utile fare un ripasso generale, vedendo le cose in modo un po’ diverso da quello che si fa a scuola. Pensateci su un attimo: perché 3×5 e 5×3 sarebbero la stessa cosa? Anzi, forse è meglio partire da una domanda precedente: cos’è esattamente la moltiplicazione?

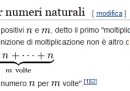
Partiamo da quello che viene insegnato alle elementari: la moltiplicazione è un’addizione ripetuta. Una specie di scorciatoia, insomma. La cosa divertente è che Wikipedia in italiano e in inglese non concordano su quale sia l’addizione da ripetere. Gli italiani sommano il primo termine, mentre gli inglesi sommano il secondo: questo probabilmente deriva da come pronunciamo la moltiplicazione. In inglese si dice “five times three”, letteralmente “cinque volte tre”. In italiano diciamo “cinque per tre (volte)”. Ma quello che è davvero importante è che nessuno ci assicura a priori che i due risultati siano uguali! Da questo punto di vista l’insegnante che ha segnato come errore 5+5+5 ha insomma ragione, se non ha ancora dimostrato agli studenti che vale quell’uguaglianza. E come lo si dimostra? Semplice: si fa il disegnino. Purtroppo il fatto stesso che i due fattori si chiamino in modo diverso (moltiplicatore e moltiplicando) contribuisce a non rendere immediata la cosa e fa richiedere una dimostrazione, ancorché semplicissima. Almeno a prima vista prendere tre mele per cinque volte a prima vista non sembra infatti lo stesso che prendere cinque mele per tre volte.

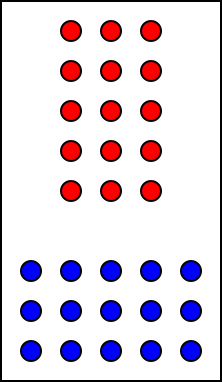Ecco qua. Basta ruotare di 90 gradi il rettangolo 5×3, quello rosso in alto, e otteniamo un rettangolo 3×5, quello blu in basso. Tra l’altro, questo è il modo in cui immagino sia nato l’idea stessa di commutatività della moltiplicazione ai tempi degli antichi greci (Euclide usa il concetto negli Elementi, anche se non lo esplicita: tutta questa storia di definizioni nasce nel XIX secolo quando si comincia a formalizzare l’aritmetica come base della matematica). Mettere i sassolini in una direzione o nell’altra cambia poco, ed è per questo che io continuo ad avere fortissimi dubbi sull’errore segnato al ragazzo per aver invertito righe e colonne. Dal mio punto di vista gli schieramenti – mi dicono che è il termine tecnico per queste configurazioni – sono uguali da qualunque parte li si veda. Certo che con l’addizione è tutto più facile. È immediato che prendere tre mele e poi aggiungerne altre cinque è la stessa cosa che prendere cinque mele e poi aggiungerne tre, no?

No. Nella vita reale ci sono casi in cui se bisogna aggiungere due cose A e B occorre fare attenzione all’ordine. La cosa si nota soprattutto in cucina: conscio della mia ignoranza nel campo ho chiesto al mio social network di riferimento di trovarmi qualche esempio e mi è stato detto che

• Per fare la besciamella il latte va aggiunto a farina+burro e non viceversa
• In alcuni composti fluidi e nella maionese gli albumi montati a neve vanno aggiunti dopo, se no si smonta tutto
• Poiché il sale è igroscopico, se quando cuoci la carne lo metti prima avrai più sugo ma carne più secca
• Se nell’insalata metti prima l’olio, il sale non si scioglie e l’aceto scivola via senza aderire alle foglie
• Quando prepari l’acqua gasata con SodaStream, prima devi mettere l’acqua e poi l’anidride carbonica

Potete insomma vedere come la commutatività dell’addizione, una proprietà che pare ancora più ovvia di quella nel caso della moltiplicazione, è un concetto che diamo probabilmente per scontato in matematica ma non certo nel mondo reale. Non riesco proprio a capire perché insomma – naturalmente dopo aver mostrato che l’ordine è irrilevante – dovremmo insegnare un ordine specifico per la moltiplicazione di numeri, solo perché la moltiplicazione di matrici non è commutativa: se e quando ci arriveranno si saranno già accorti che dare lo stesso nome a due operazioni fondamentalmente diverse non significa che le due operazioni siano davvero equivalenti.

Ma c’è di più! Chi ha mai detto che la moltiplicazione è un’addizione ripetuta? Proseguendo nel percorso scolastico si scoprirà infatti che esiste anche un altro tipo di moltiplicazione, inizialmente presentata mentre si studia fisica: la dilatazione. Si, si può dire che moltiplicare per due un vettore significa mettere due copie una davanti all’altra e vedere cosa succede; ma in pratica il risultato lo si pensa come una dilatazione di un fattore 2. Ovviamente si può “dilatare” anche restringendoci, cioè moltiplicando per un fattore minore di 1; e addirittura “dilatare” dall’altra parte, quando si moltiplica per −1 e si cambia verso al vettore. Se ci pensate, è la stessa cosa che facciamo quando giochiamo con un cursore e lo facciamo girare dall’altra parte. Niente schieramenti e addizioni ripetute: la moltiplicazione in questo caso diventa un’operazione che funziona per conto suo e non si appoggia su nessun’altra, anche se devo riconoscere che in questo caso dimostrare la sua commutatività non è più banale come mostrato sopra.

Qual è la morale di questa storia? Semplice: le operazioni, anche quelle che usiamo tutti i giorni, non sono poi così una cosa così naturale come forse immaginiamo. Tornando al problema di partenza, penso che probabilmente, invece che segnalare le soluzioni non ufficiali come errate, sarebbe preferibile fermarsi e cercare di capire se il ragazzo ha effettivamente capito cosa sta facendo. È più lungo, ma più rispettoso dello studente…

P.S.: mentre cercavo informazioni per scrivere questo post ho trovato questo documento che in parte non condivido ma penso dia degli ottimi spunti di riflessione sui problemi nel vedere la moltiplicazione come addizione ripetuta. Buona lettura!