Numeri che appaiono in posti impensati [Pillole]
Ci sono alcuni numeri interi che possono essere espressi come somma di due quadrati di numeri interi: per esempio, 10 = 1 + 9 = 12 + 32 (e le altre tre possibilità che si hanno cambiando il segno a uno o entrambi gli addendi: (−1,3), (1,−3), (−1,−3). Altri numeri, come 11, non ammettono nessuna scomposizione come somma di due quadrati. Il numero Q(n) di scomposizioni possibili varia molto: i primi valori di Q(n), per n che va da 0 a 10, sono 1, 4, 4, 0, 4, 8, 0, 0, 4, 4, 8 (vedi OEIS). Quello che può sembrare incredibile è che il valore medio di Q(n), per n che tende all’infinito, vale esattamente π.
25 può essere espresso in 12 modi come somma di quadrati
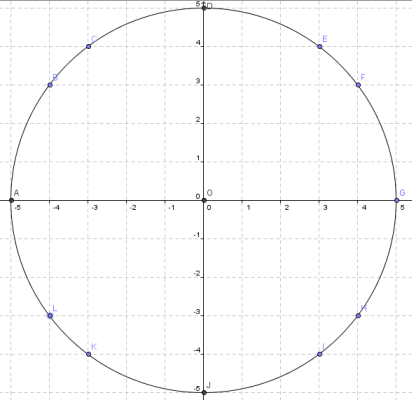
Il fatto sembra incredibile, ma la sua dimostrazione è molto semplice. La somma dei Q(i) per i che va da 0 a n è pari al numero di punti del reticolo degli interi che sono contenuti nel cerchio di centro l’origine e raggio √n; tale numero di punti tende a essere pari all’area del cerchio stesso, cioè πn. Dividiamo per n per ottenere il valore medio, e siamo a posto.
