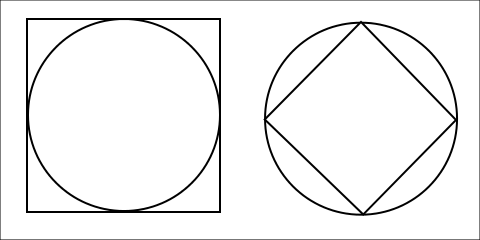
Quante palle!
Un problemino che a dire il vero non ho mai trovato molto interessante è chiedere se è meglio mettere un tappo quadrato in un foro rotondo oppure un tappo rotondo in un foro quadrato. Supponendo che i tappi siano della massima dimensione possibile, nel senso che se crescessero ancora non entrerebbero più nel foro, la risposta è semplice: un cerchio di raggio 1 viene inscritto in un quadrato di raggio 2, quindi la parte di area che viene tappata è 4/π; un quadrato di diagonale 2 viene inscritto in un cerchio di raggio 1, quindi la parte di area che viene tappata è π/2. Considerando che il medio proporzionale tra 2 e 4 è √2 che è minore di π è chiaro che è meglio mettere il tappo rotondo nel foro quadrato. Detto tutto questo, il problemino continua a sembrarmi stupido, perché in nessun caso sto davvero tappando.
quale tappo è il migliore?
