La parità all’opera
Un problema molto carino che ho trovato sul libro di Peter Winkler Mathematical Puzzles ha il testo seguente:
Supponiamo di avere un rettangolo diviso in un certo numero di rettangoli, per ciascuno dei quali o la base o l’altezza (oppure entrambe) hanno una lunghezza intera. Dimostrare che anche il rettangolo grande ha la stessa proprietà, cioè almeno uno dei suoi lati ha lunghezza intera.
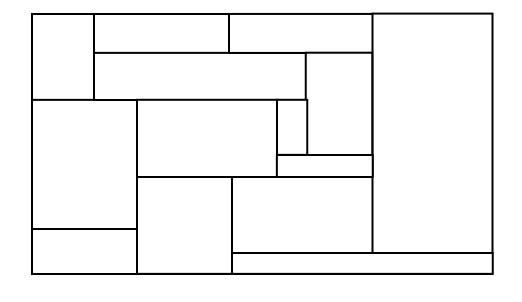
Se volete provare a dimostrarlo per conto vostro, fate pure: io non ci sono riuscito, e sono andato a consultare la soluzione, che troverete qui sotto. Eppure la soluzione, quando la vedete, non è per nulla complicata. Come mai allora non è facile trovarla? Semplice: bisogna applicare una tecnica che a prima vista non c’entra nulla.



