Che cos’è davvero il problema dei tre corpi
Il romanzo di fantascienza di Liu Cixin da cui è tratta la nuova serie di Netflix affronta un'affascinante quanto caotica questione sulle orbite dei corpi celesti
di Emanuele Menietti

Il problema dei 3 corpi è la nuova serie di fantascienza di Netflix, tra le più attese dell’anno e ispirata all’omonimo romanzo dello scrittore cinese Liu Cixin. Il titolo fa riferimento a una delle questioni più note e discusse della meccanica celeste, la disciplina che studia il movimento di pianeti, satelliti, asteroidi e altri corpi con un approccio fisico-matematico. Il “problema dei tre corpi” vero e proprio è centrale nel racconto del libro e ha una certa importanza anche nella serie televisiva, che si è però presa qualche licenza distanziandosi in parte dalle vicende immaginate da Liu Cixin.
Da qui in avanti ci sono piccoli spoiler sul romanzo necessari per contestualizzare la spiegazione che verrà dopo, non rivelano cose che non si intuiscano dal titolo stesso del libro o della serie televisiva: chi proprio non ne vuole sapere nulla può saltare i prossimi due paragrafi.
Nel romanzo
Il libro racconta spostandosi tra passato, presente e futuro un contatto dell’umanità con una civiltà aliena che vive in un sistema solare diverso dal nostro. Uno dei protagonisti della storia scopre quello che sembra essere un videogioco nel quale si deve provare a far sopravvivere una civiltà che vive su un pianeta particolare, dove si susseguono “Ere dell’ordine” dove l’alternarsi del dì e della notte e delle stagioni è regolare e periodi in cui ci sono “Ere del caos”, dove stagioni e giornate hanno durate molto diverse e irregolari. Nelle “Ere dell’ordine” la civiltà prospera e si sviluppa, mentre nelle “Ere del caos” viene sterminata dalle condizioni invivibili in cui finisce il pianeta.
Le simulazioni del videogioco proseguono per buona parte del libro, mentre succedono intanto altre cose su piani narrativi ed epoche diverse che aiutano a capire cosa sia davvero quel gioco. Diventa quindi chiaro che la difficoltà sta nel fatto che il mondo del videogioco è situato in un sistema a tre stelle, che interagiscono gravitazionalmente tra loro e influenzano in questo modo anche l’orbita del pianeta che alterna fasi più stabili ad altre in cui subentra il caos, con inverni gelidi e lunghissimi, giorni con momenti di luce che durano pochi istanti o che si protraggono a lungo, determinando la fine (o per meglio dire la sospensione) di buona parte della vita.
Il problema dei tre corpi
Il problema dei tre corpi consiste proprio nella difficoltà di prevedere con accuratezza il modo in cui si muovono tre corpi celesti e l’evoluzione del sistema che costituiscono. È una questione che appassiona da secoli matematici, astronomi e astrofisici e che a differenza di quanto si immagina non è sempre irrisolvibile. Approfondendola, negli anni è stato possibile capire meglio come funzionano le orbite dei corpi celesti e soprattutto capire come sfruttarle, per esempio per gestire missioni spaziali interplanetarie con sonde realizzate per esplorare il nostro sistema solare.
Come impariamo a scuola, il Sole è di gran lunga l’oggetto più massiccio nel nostro sistema solare e visto che la capacità di attrarre altri corpi (interazione gravitazionale, nel senso della fisica classica, o più semplicemente quella che chiamiamo “forza di gravità”) dipende fortemente dalla massa, il Sole riesce a tenersi stretti (in termini cosmici) i pianeti e a farli orbitare intorno a sé. Anche i pianeti producono interazioni gravitazionali tra loro, ma queste sono tutto sommato trascurabili perché la loro massa è incomparabile con quella del Sole (la massa di quest’ultimo è per esempio più di 330mila volte quella della Terra).
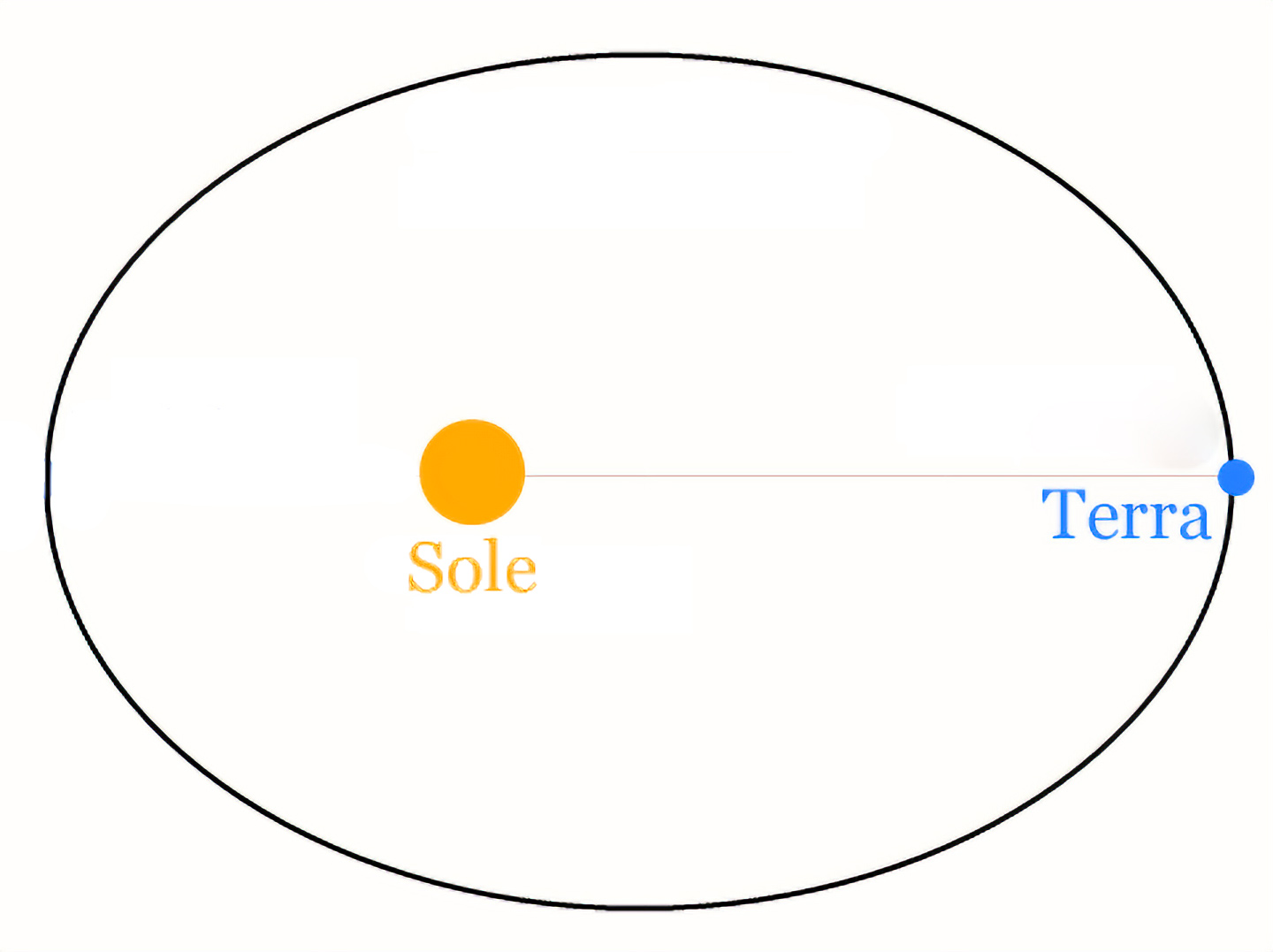
Alla fine del Seicento, il matematico e fisico inglese Isaac Newton formalizzò le equazioni sul moto e la gravità dei corpi celesti, in modo da poter calcolare in linea di principio il punto in cui si troverà un corpo che orbita intorno a un altro in un dato momento conoscendo la posizione di partenza, la velocità e poche altre variabili. Le leggi del moto di Newton si basavano sul lavoro e sugli studi svolti in precedenza da altri importanti scienziati come l’astronomo tedesco Keplero, che aveva formulato le leggi che regolano i movimenti dei pianeti.
Utilizzando le leggi e le equazioni di Newton si possono calcolare esattamente le orbite descritte da due corpi legati da un’interazione gravitazionale. Le forme di queste orbite possono essere un cerchio, un’ellissi, una parabola e qualsiasi altra sezione conica (le forme che si possono ottenere affettando un cono). La Terra, per esempio, descrive un’orbita ellittica intorno al Sole.
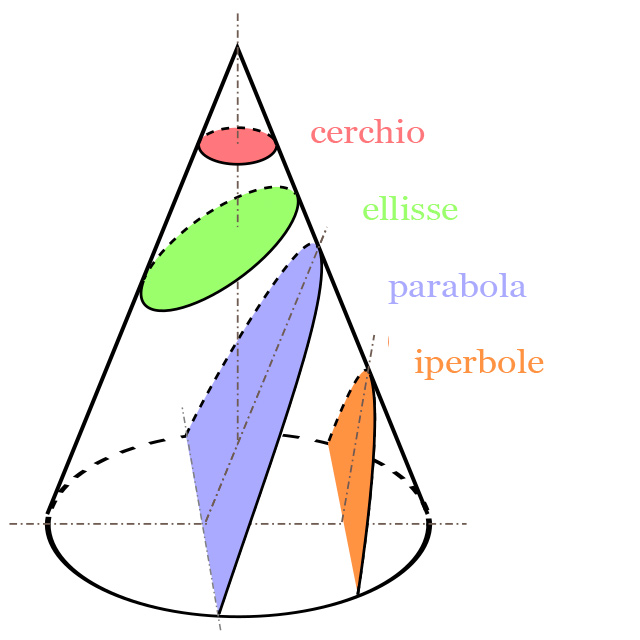
(Wikimedia)
Le leggi di Newton forniscono soluzioni semplici quando si prende in considerazione uno scenario in cui ci sono solamente due corpi celesti che interagiscono tra loro in tutto l’Universo: un “sistema a due corpi”. Appena si prova ad aggiungere un terzo corpo, le cose si complicano enormemente con le orbite che diventano irregolari e spesso imprevedibili nel lungo periodo. In questo caso conoscere la posizione di partenza dei corpi e la loro velocità non è più sufficiente per fare previsioni accurate perché diventa tutto caotico, e quasi sempre dopo un certo periodo di tempo uno dei tre corpi viene espulso dal sistema.
A dirla tutta qualsiasi sistema con più di due corpi è problematico e per questo si parla in generale di “problema degli n-corpi”, dove “n” indica appunto un numero qualsiasi. È una questione che ha appassionato e tenuto occupati tantissimi matematici, fisici e astronomi dai tempi di Newton, quando ci si iniziò a chiedere come prevedere le orbite di corpi celesti in sistemi più complessi. Non era solamente una questione teorica: la previsione dei movimenti della Luna e dei pianeti era per esempio essenziale per la navigazione in mare e in tempi più recenti lo è diventata per organizzare le missioni spaziali.
Fu evidente piuttosto in fretta che almeno per il nostro vicinato cosmico il problema degli n-corpi non fosse insormontabile, a patto di accontentarsi di un certo grado di approssimazione. Un sistema con più corpi celesti sufficientemente distanti tra loro può essere infatti immaginato come una serie di sistemi a due corpi. Nel caso del sistema solare questo lavoro è facilitato dalla presenza di un’unica stella, il Sole, che come abbiamo visto ha una forte influenza su tutto il resto per via della sua enorme massa. Si possono quindi considerare con approssimazione sistemi di due corpi che comprendono sempre il Sole e uno degli altri pianeti, trascurando tutto il resto.
In questo modo si ottiene un sistema solare in cui ogni pianeta compie un’orbita ellittica intorno al Sole come previsto dalle leggi di Keplero. È un’approssimazione più che accettabile per l’orizzonte temporale delle nostre esistenze e tutto sommato dell’intero genere umano, considerato che gli eventuali cambiamenti delle orbite dovuti a minime interazioni gravitazionali diventano apprezzabili in milioni se non miliardi di anni.
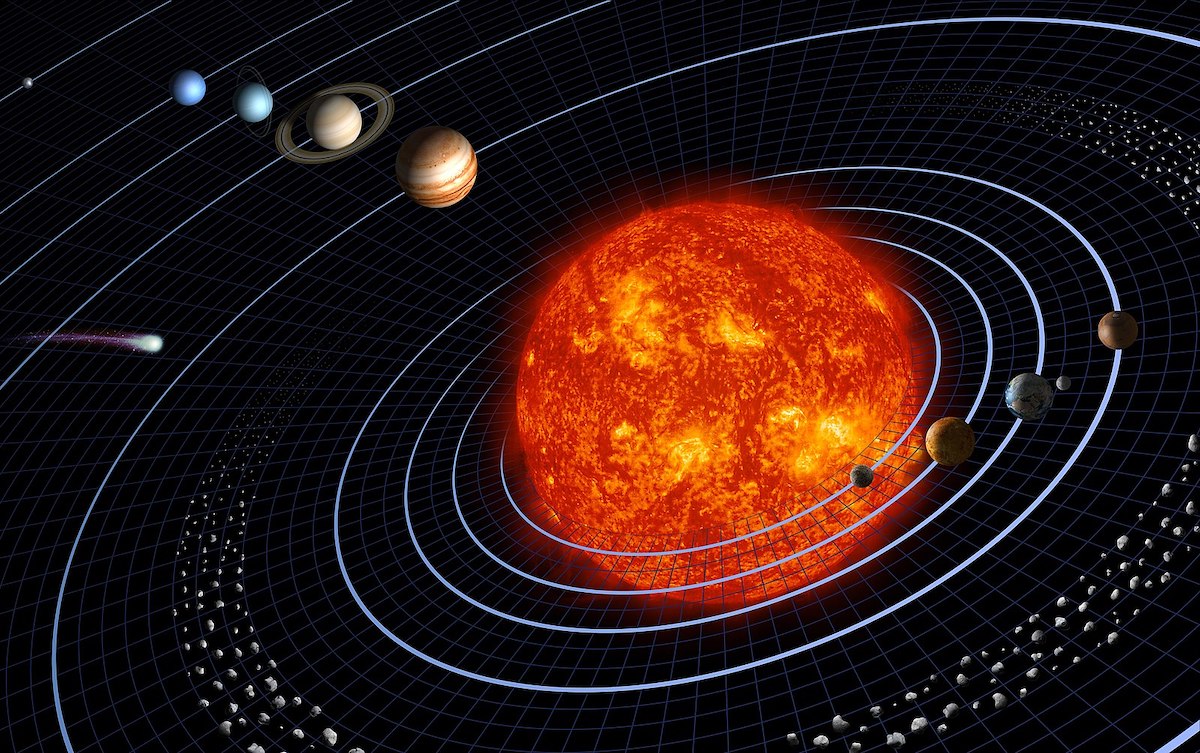
Rappresentazione non in scala del sistema solare (NASA)
Queste soluzioni non perfette rientrano nel cosiddetto “problema dei tre corpi ristretto”, dove si accetta di avere la migliore approssimazione possibile del moto dei corpi celesti. Nel caso del sistema solare lo si fa assumendo per esempio che abbiano una massa trascurabile rispetto al Sole e anche rispetto a Giove, il pianeta più grande nella famiglia degli otto pianeti propriamente detti compresa ovviamente la Terra.
Per chi ne studia le orbite, il nostro sistema solare offre inoltre il vantaggio di avere una sola stella, a differenza di molti altri sistemi dove si contano un paio di stelle (“sistemi binari”). I soli di questi ultimi formano solitamente orbite stabili intorno a un determinato punto che corrisponde al loro centro di massa. I pianeti dei sistemi binari hanno solitamente orbite stabili a loro volta, per distanza e minore massa rispetto alle stelle, e si possono quindi prevedere con una buona approssimazione i loro movimenti nel tempo.
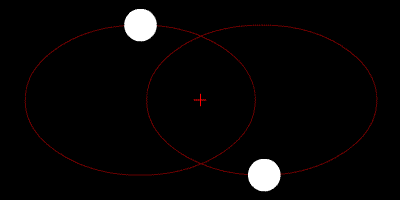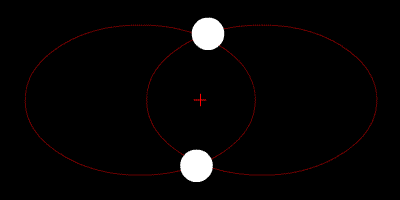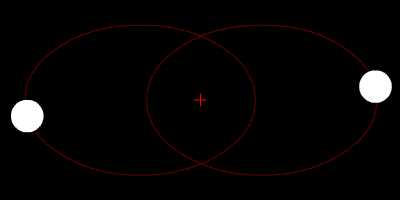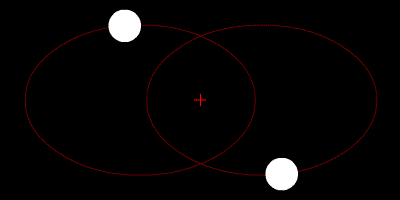
Ci sono comunque metodi per lavorare sul problema dei tre corpi e ottenere risultati il più possibile aderenti alla realtà. Una porzione molto piccola di traiettoria può essere calcolata con precisione, di conseguenza se si scompone l’intero problema in piccole sezioni si possono calcolare i movimenti di tutti i corpi nel sistema in un breve intervallo di tempo e aggiornarli man mano che si calcolano le sezioni successive (in termini matematici si dice che si effettuano integrazioni numeriche per risolvere equazioni differenziali).
Applicando questa tecnica si ottiene una simulazione di n-corpi, cioè una simulazione per prevedere i movimenti di un certo numero di pianeti in un futuro anche molto lontano. Le simulazioni possono essere utilizzate per provare a prevedere la formazione o l’evoluzione di intere galassie, cioè di un grande insieme di sistemi solari, stelle, polveri e gas interstellari. Oggi questi calcoli vengono effettuati con computer molto potenti, mentre un tempo dovevano essere effettuati a mano con molta pazienza e il rischio di fare qualche errore in più.
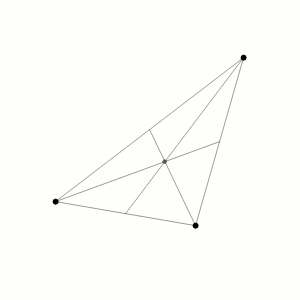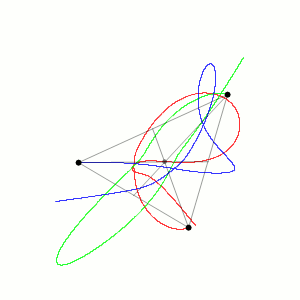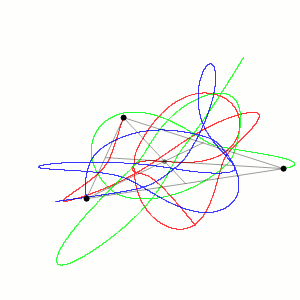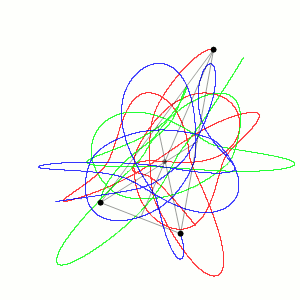
Approssimazione delle traiettorie di tre corpi identici, il cui centro di massa rimane fisso (Wikimedia)
Diversi matematici e astronomi si confrontarono con il problema dei tre corpi per trovare casi specifici in cui fosse possibile una soluzione del tutto funzionante e senza approssimazioni (cioè una soluzione analitica). Il matematico svizzero Eulero nel diciottesimo secolo trovò una serie di soluzioni per tre ipotetici corpi celesti che rimangono sempre allineati lungo una retta immaginaria che attraversa il loro centro di massa. L’italiano Joseph-Louis Lagrange trovò una soluzione ancora più elegante al problema dei tre corpi, calcolando i punti nello spazio nei quali due corpi con massa molto grande permettono a un terzo corpo (con una massa molto inferiore) di mantenere una posizione stabile relativamente agli altri due. Questi punti oggi sono proprio noti come “punti di Lagrange” e sono essenziali per collocare nello Spazio a grande distanza dalla Terra sonde e telescopi per scopi di ricerca.

I punti di Lagrange (NASA)
L’avvento dei computer e la possibilità di avere sistemi di calcolo sempre più potenti hanno offerto negli ultimi anni nuove opportunità per affrontare il problema degli n-corpi. Nel 2009, un gruppo di ricerca effettuò una simulazione che fece discutere tra gli esperti e appassionati di orbite: raccolse quante più informazioni possibili sul nostro sistema solare e provò a prevedere che cosa sarebbe potuto accadere a ogni pianeta che lo costituisce nei prossimi 5 miliardi di anni.
Il gruppo di ricerca effettuò più di 2mila simulazioni partendo sempre dalle stesse identiche condizioni tranne una: la distanza tra il Sole e Mercurio, il pianeta più vicino alla nostra stella. In ogni simulazione la distanza veniva modificata di pochi millimetri per vedere se nel lunghissimo periodo questa differenza potesse avere qualche conseguenza per il resto dei pianeti (tra il Sole e Mercurio ci sono in media 58 milioni di chilometri). Nell’1 per cento delle simulazioni l’orbita di Mercurio nel tempo cambiava al punto da poter far collidere il pianeta con il Sole o con il suo altro vicino più prossimo: il pianeta Venere. In una simulazione la modifica iniziale dell’orbita di Mercurio era invece sufficiente per destabilizzare l’intero sistema solare interno, che oltre a Mercurio e Venere comprende la Terra, Luna, Marte e i suoi due satelliti.
La ricerca è un buon esempio delle difficoltà poste dal problema degli n-corpi. Il sistema in sé non è infatti completamente casuale: se in più simulazioni si parte sempre dalle stesse condizioni di partenza si ottiene sempre il medesimo risultato, ma se si modifica una variabile anche solo di un valore minuscolo nel lungo periodo il risultato cambia: è la definizione di sistema caotico. La quantità di variabili è tale da complicare i calcoli al punto da rendere impossibile avere una soluzione generale al problema, che si applichi a tutti i casi possibili.
Come abbiamo visto il problema può essere in qualche modo governato, ma non è comunque una questione da poco e dove si incontrano limiti di questo tipo subentrano spesso le considerazioni filosofiche. Ma del resto, per dirla come scrive Liu Cixin nel suo romanzo: «Dovrebbe essere la filosofia a guidare gli esperimenti, o dovrebbero essere gli esperimenti a guidare la filosofia?».



