Costruire nuove strade è un problema matematico non da poco

A un gruppo di abitudinari automobilisti che si ritrova periodicamente bloccato in un ingorgo stradale verrebbe spontaneo pensare che le condizioni del traffico migliorerebbero se venisse aperta una nuova strada oltre a quella che stanno percorrendo. Nella pratica, però, per quanto possa sembrare controintuitivo, aprire una nuova strada potrebbe causare un peggioramento dell’ingorgo.

È un effetto noto come paradosso di Braess, dal nome del matematico tedesco che lo teorizzò negli anni Sessanta: Dietrich Braess. Ed è utilizzato anche per spiegare il caso contrario: la possibilità, attestata da esempi concreti, che la chiusura di una strada possa ridurre il traffico.

Il paradosso di Braess, di cui ha scritto recentemente il giornale online norvegese Forskning.no, è soltanto uno dei vari fenomeni tenuti in considerazione quando vengono pianificate nuove strade per migliorare la viabilità e ridurre il rischio di congestione del traffico, che dipende da numerose variabili difficili da calcolare. È però una teoria utile a comprendere un fatto fondamentale: le persone alla guida tendono a vedere soltanto i propri “costi” e non gli effetti negativi del loro comportamento sul sistema di cui fanno parte. La gestione di questo sistema – non soltanto la costruzione di nuove strade, ma anche l’utilizzo di pedaggi, dissuasori e altri strumenti possibili – ne tiene conto e fa in modo che le scelte individuali non finiscano per penalizzare tutti gli automobilisti.

La prima descrizione sistematica del paradosso di Braess risale alla pubblicazione del suo studio del 1968 Über ein Paradoxon aus der Verkehrsplanung (“Su un paradosso della pianificazione del traffico”), pubblicato mentre lavorava all’università della Ruhr a Bochum allo sviluppo di un nuovo modello teorico di spiegazione del traffico. Braess osservò che all’interno di una rete stradale i tempi di percorrenza ottimali non sempre si ottengono se ogni conducente sceglie il percorso a lui più conveniente. E concluse che sulla base di questa premessa esistono casi in cui l’espansione della rete può portare a tempi di percorrenza complessivi più lunghi.

Per comprendere il paradosso viene di solito proposto un esempio matematico in cui occorre spostarsi da un punto A a un punto B, ma non è possibile farlo direttamente: serve passare o per un punto c o per un punto d. Sia in un percorso che nell’altro sono presenti un tratto con un’ampia carreggiata il cui tempo di percorrenza è invariabilmente 20 minuti e un tratto più stretto il cui tempo di percorrenza dipende dal traffico. Questa variabile è espressa dal numero di veicoli (T) presenti su quel tratto diviso 10 (se i veicoli sono 100, per esempio, il tempo di percorrenza sarà 10 minuti, ma se sono 500 sarà 50 minuti).

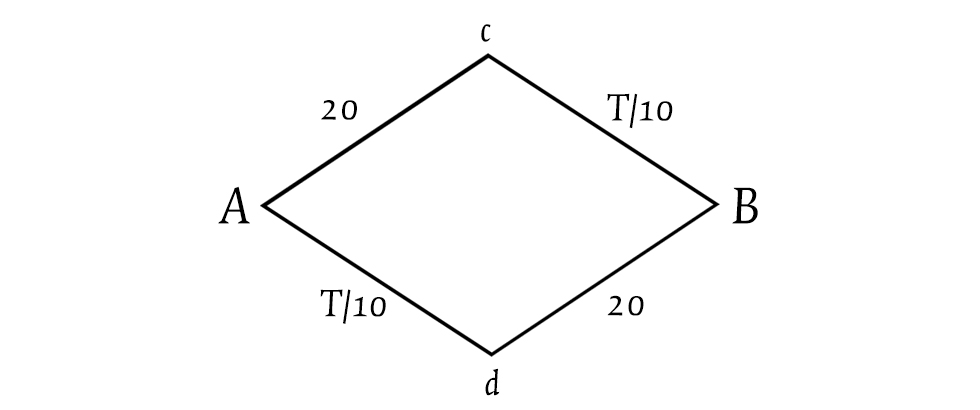
Immaginando che ci siano 200 automobilisti che devono spostarsi lungo la rete da A a B, alla lunga la situazione si stabilizzerà in una divisione del gruppo in cui 100 automobilisti seguono un percorso e 100 seguono l’altro. E il tempo di percorrenza complessivo per tutti sarà di 30 minuti (perché 100 diviso 10 fa 10 minuti). A questo punto ci si chiede cosa potrebbe succedere nel caso ipotetico in cui venisse aperta tra i due punti intermedi c e d una nuova strada, un collegamento “ideale” che non richieda alcun tempo di percorrenza (0 minuti).

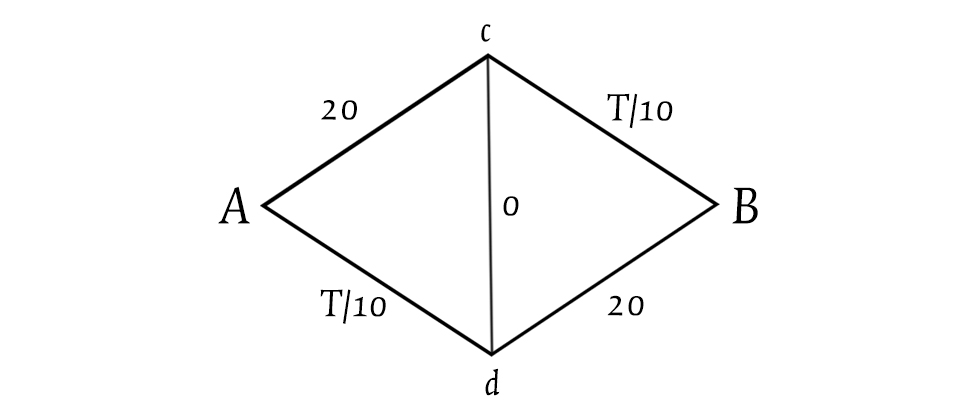
I 200 automobilisti avrebbero l’opportunità di utilizzare questo collegamento per percorrere due tratti T/10 anziché uno. La percorrenza del tratto T/10 è infatti inferiore o uguale a 20 minuti (perché il traffico complessivo è di 200 automobilisti), ma mai superiore, e quel tratto è quindi preferibile rispetto al tratto il cui tempo di percorrenza è invariabilmente 20 minuti. Tutti prenderanno allora il collegamento tra i due punti intermedi, ma in questo modo il tempo di percorrenza complessivo da A a B sarà 40 minuti (20 + 20): paradossalmente, più del tempo necessario prima che venisse aperto il collegamento.

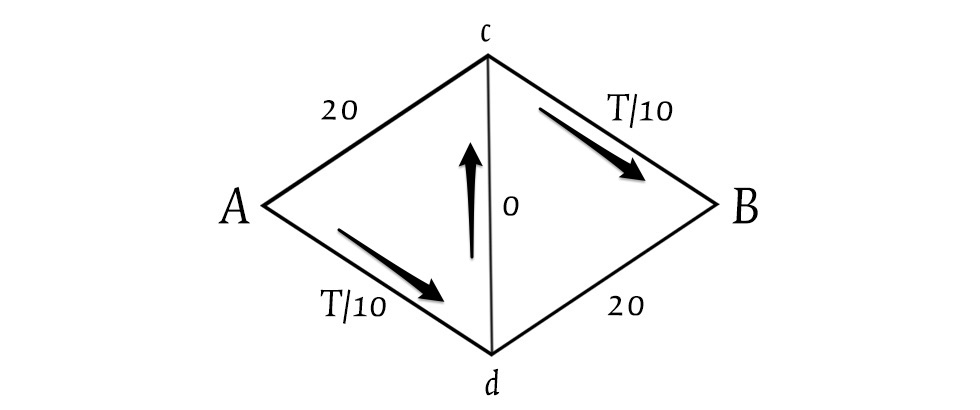
Se ogni automobilista prende la decisione ottimale egoistica su quale sia il percorso più veloce, scrisse Braess, «un’estensione della rete stradale può provocare una ridistribuzione del traffico che si traduce in tempi di percorrenza individuali più lunghi».

La spiegazione del paradosso di Braess, un fenomeno noto e studiato anche in economia, richiama in particolare nozioni relative alla cosiddetta “teoria dei giochi”. È l’area della matematica che attraverso modelli semplificati della realtà si occupa dello studio e dell’analisi delle interazioni tra due o più soggetti interessati a ottenere il massimo vantaggio possibile da queste interazioni.

Il caso della rete stradale in cui gli automobilisti cercano di raggiungere dal punto A il punto B nel minor tempo possibile è un esempio di gioco non cooperativo: ciascun automobilista non conosce le strategie degli altri e cerca di seguire quella che ritiene essere la più vantaggiosa per sé. Ma non è detto che sia la più vantaggiosa in assoluto, come dimostra il paradosso. La particolare condizione del gioco in cui ogni partecipante non ha alcun incentivo a cambiare strategia, perché ci perderebbe, è definita equilibrio di Nash, dal nome del matematico statunitense e premio Nobel per l’Economia John Nash (la cui storia fu peraltro resa nota nel film del 2001 A Beautiful Mind).

La condizione iniziale nel paradosso di Braess, cioè i 200 automobilisti distribuiti equamente tra i due percorsi, è un equilibrio di Nash. Nessun automobilista infatti ha interesse a cambiare strada: se lo facesse, impiegherebbe più tempo per arrivare a B, dal momento che il tempo di percorrenza del tratto variabile (T/10) diventerebbe 101/10 (10,1 minuti invece che 10). L’apertura del collegamento tra i due punti intermedi determina un nuovo equilibrio di Nash in cui tutti prendono la stessa strada, perché singolarmente non avrebbero niente da guadagnare scegliendone una diversa.

Aumentare le capacità della rete in una situazione in cui le entità in movimento scelgono egoisticamente quale sia il percorso migliore, secondo Braess, può quindi portare in alcuni casi a un peggioramento delle prestazioni complessive della rete, perché l’equilibrio di Nash di un sistema di questo tipo non è necessariamente quello ottimale.

In altri casi l’aggiunta di corsie a una strada esistente può generare un traffico indotto, una specie di “induzione della domanda” applicata al campo dei trasporti. Tende a verificarsi quando nuove strade vengono progettate e costruite, più che per tentare di risolvere un problema di traffico esistente, in previsione di un aumento del traffico futuro determinato da variabili come la crescita economica o il maggior numero di macchine vendute.

In casi del genere può succedere che la costruzione di una nuova strada non si limiti a soddisfare una domanda latente di viaggi in macchina, repressa a causa di limitazioni esistenti nell’infrastruttura, ma porti anche a un aumento del traffico indotto. Gli automobilisti, in altre parole, potrebbero scegliere di viaggiare in macchina in casi in cui non lo avrebbero fatto altrimenti.

– Leggi anche: Perché si formano gli ingorghi sulle strade

Sebbene il modello teorico su cui si basa sia una rappresentazione molto semplificata della realtà, il paradosso di Braess è stato utilizzato anche per spiegare empiricamente casi storici in cui le prestazioni di una rete stradale malfunzionante migliorarono a seguito della riduzione anziché dell’espansione della rete.

A Seul, in Corea del Sud, la demolizione di un’autostrada a sei corsie negli anni Duemila, necessaria per la costruzione di un parco pubblico, ridusse i tempi di viaggio dentro e fuori la città (senza ridurre significativamente il volume complessivo del traffico, cioè la quantità di macchine in movimento). Nel 1990 la chiusura provvisoria della 42^a strada a New York per la Giornata della Terra, il 22 aprile, determinò una riduzione degli ingorghi. E uno studio pubblicato nel 2008 sulla rivista Physical Review Letters individuò alcune strade a Boston, New York e Londra la cui chiusura avrebbe ridotto i tempi di viaggio previsti per alcuni percorsi.

Nella pratica, però, come per altri fenomeni controintuitivi, occorre una combinazione di condizioni molto rare perché il paradosso di Braess si verifichi concretamente. E sono molto rare anche perché questo fenomeno è ampiamente noto e tenuto in considerazione da decenni in fase di gestione della viabilità e progettazione delle strade. «L’importante quando si pianifica un nuovo sviluppo della rete stradale è effettuare simulazioni e verificare se questo fenomeno si verifica», ha detto a Forskning.no Helge Holden, docente di matematica alla Norwegian University of Science and Technology (NTNU) a Trondheim.

A Oslo, in Norvegia, un possibile caso di paradosso di Braess citato da Forskning.no fu evitato negli anni Novanta grazie a una consulenza fornita all’amministrazione della città dal Transportøkonomisk institutt (TØI), un istituto nazionale di ricerca multidisciplinare sui trasporti. L’idea di costruire una corsia in più dopo due lunghe gallerie (Granfosstunnelen) sulla tangenziale 150 fu messa da parte perché, secondo le simulazioni effettuate dall’istituto, avrebbe causato un aumento del traffico anziché una distribuzione su più strade.

Le ricerche nell’ambito della gestione del traffico stradale suggeriscono che la costruzione o la chiusura delle strade possono condizionare in modi non facilmente prevedibili le numerose variabili alla base della formazione degli ingorghi. Alcune persone potrebbero per esempio cambiare non soltanto il percorso ma anche le abitudini e gli orari di viaggio. E per simulare i vari flussi di traffico nel caso di chiusura di una o più strade – per convertirle in piste ciclabili, per esempio – occorre molta potenza di calcolo, ha detto Stefan Flügel, ricercatore del TØI.