Il “cappello” a un annoso problema matematico
Sembra sia stato infine scoperto un "einstein", cioè una forma che può ricoprire una superficie infinita senza mai ripetere lo stesso motivo
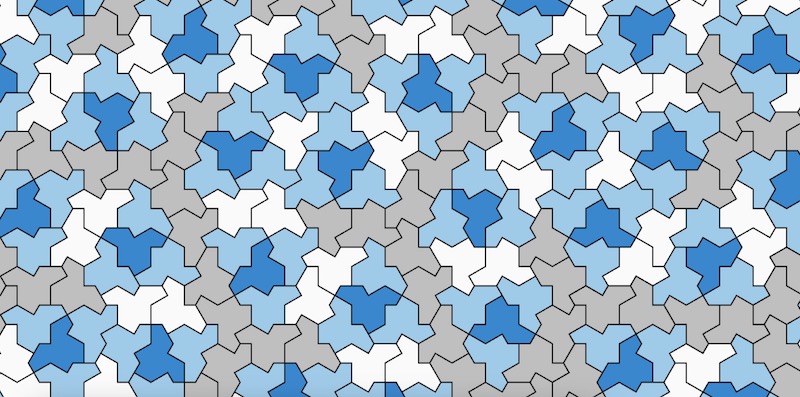
Immaginiamo che Roger abbia comprato un monolocale con una metratura infinita e voglia posarci un pavimento di piastrelle. Roger però è un tipo particolare e vuole che per l’intero pavimento siano utilizzate piastrelle tra loro tutte uguali e che accostate producano un motivo che non si ripete mai uguale (aperiodico), all’infinito. In altri termini, Roger è alla ricerca di un “einstein”, non nel senso di Albert Einstein, ma di un “tassello non periodico”, una forma che riempia il piano geometrico con un motivo che non si ripete mai allo stesso modo. La parola einstein in questo caso deriva dal tedesco “ein Stein”, letteralmente “una pietra”, intesa con una certa approssimazione come una piastrella o ancora più in generale una forma.
Quello di Roger è un problema matematico, perché un comune pavimento di piastrelle può teoricamente proseguire all’infinito, ma intere sue sezioni potranno sempre essere sovrapposte perfettamente l’una sull’altra perché si ripetono in qualche modo: per quanto sia enorme ed esteso un singolo motivo, infatti, prima o poi accade sempre. Nel caso dei tasselli non periodici invece questa perfetta sovrapposizione non può essere effettuata, ma non è semplice trovare le giuste forme dei tasselli per poterlo fare. Specialmente se si vuole utilizzare sempre e solo una forma, un einstein appunto. Fino a qualche tempo fa sembrava essere un problema irrisolvibile, ma ora un appassionato di matematica e geometria dice di esserci riuscito e le dimostrazioni che ha presentato sono piuttosto convincenti.
L’annuncio ha fatto molto discutere gli esperti di tassellazioni, cioè chi studia i modi per ricoprire un piano con una o più figure geometriche che si ripetono all’infinito e senza sovrapposizioni. Farlo periodicamente, quindi con ripetizioni, è sostanzialmente la norma, ma da decenni i matematici si chiedono quali siano i modi migliori per farlo aperiodicamente. All’inizio sembrava pressoché impossibile, poi a partire dagli anni Sessanta iniziarono a esserci studi e ricerche sulla produzione di motivi non periodici utilizzando migliaia e poi centinaia di tasselli diversi tra loro.
Un importante progresso fu ottenuto negli anni Settanta dal matematico britannico Roger Penrose, quando dimostrò che con due soli tasselli fosse possibile ottenere una tassellazione di superfici infinite in modo aperiodico. Nel 2020, Penrose ha vinto il premio Nobel per la Fisica, ma per i suoi studi su oggetti molto più sfuggenti delle piastrelle: i buchi neri.
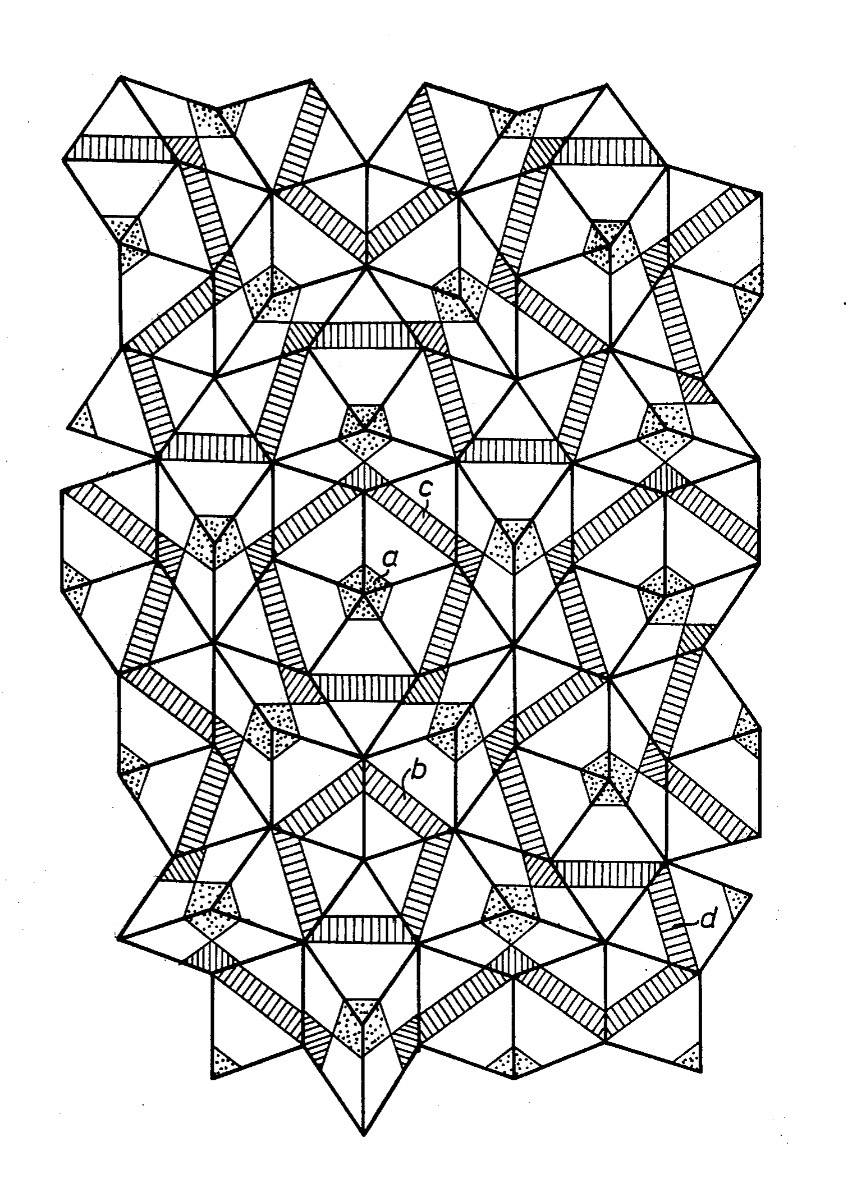
(Penrose, 1974)
Con il suo studio, Penrose aprì la strada allo sviluppo di numerose combinazioni di coppie di tasselli diversi sufficienti per raggiungere lo scopo. Il catalogo delle coppie di forme possibili divenne sempre più grande, ma i più ambiziosi continuavano a chiedersi se non ci fosse il modo di raggiungere il medesimo risultato con un solo tassello: un einstein, appunto. Tra i più interessati a riuscirci c’era David Smith, un ex tecnico di stampa britannico di 64 anni appassionato di forme geometriche e di come si dispongono sul piano.
Smith non ha una grande preparazione matematica, ma usa l’intuizione quando si tratta di lavorare con i tasselli, procedendo per prove ed errori e migliorando via via le forme che ritiene più promettenti; utilizza anche alcuni software che consentono di simulare la costruzione di poligoni. Ha stampato i più promettenti in decine di copie e ha provato poi a unirli tra loro a mano su una superficie, osservando i motivi che formano e verificando se possano o meno ripetersi dopo un certo numero di aggiunte di nuovi tasselli. È un po’ come fare un puzzle, ma senza sapere quale disegno apparirà.
Dopo molte prove e fallimenti, lo scorso novembre Smith ha elaborato un tassello che pareva fare al caso suo: non sembrava ripetere mai lo stesso motivo. Pensando di avere infine tra le mani un einstein, si mise in contatto con l’informatico Craig Kaplan dell’Univerisità di Waterloo (Canada) con il quale aveva già collaborato in passato.
Kaplan inserì la forma in un simulatore che aveva sviluppato per produrre tassellazioni sempre più grandi, notando che anche aumentandone enormemente la superficie non si creavano discontinuità sul piano: i tasselli si incastravano tra loro sempre perfettamente. In seguito Smith e Kaplan determinarono il modo in cui, partendo da una specifica tassellazione, se ne può ottenere una più grande con le stesse caratteristiche di base e capirono come il metodo potesse essere esteso potenzialmente all’infinito, ottenendo una dimostrazione sufficiente per affermare di avere infine trovato un einstein, come spiegano nella loro ricerca scritta insieme a Joseph Samuel Myers e Chaim Goodman-strauss.
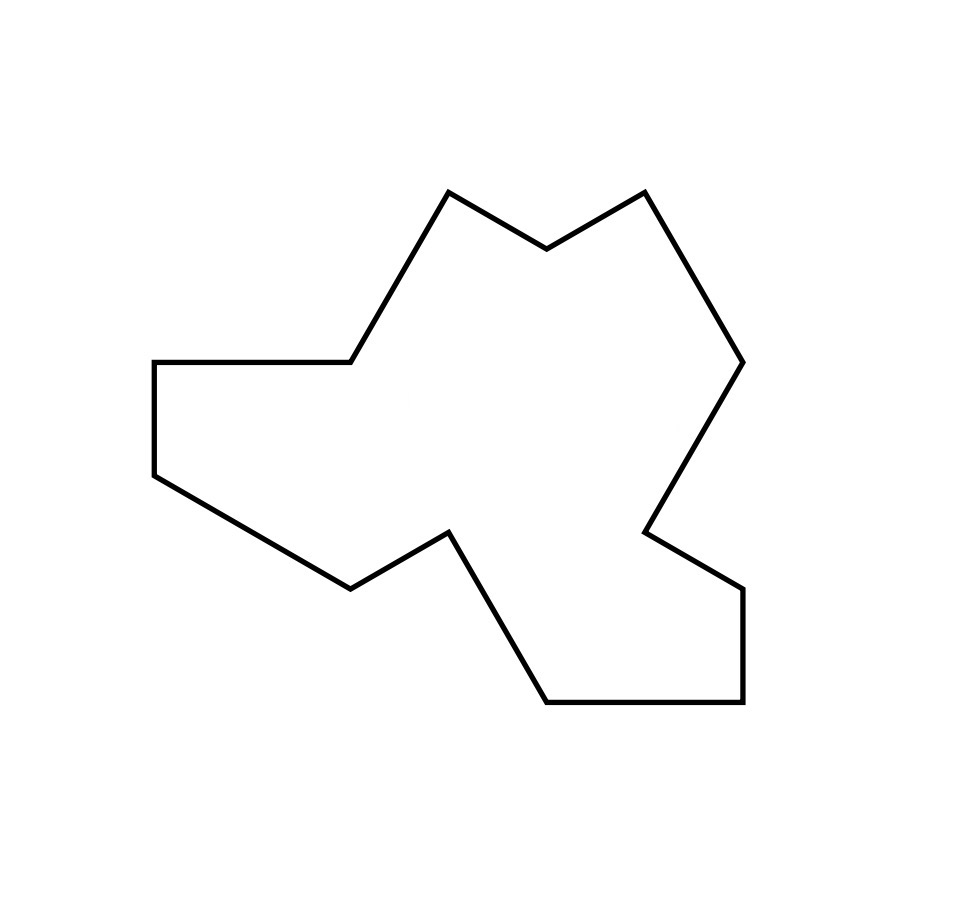
Il tassello “the hat” (“il cappello”) trovato da Smith (David Smith et al.)
Smith ha chiamato il suo tassello “the hat” (“il cappello”) perché gli ricorda un Fedora, anche se a osservarlo sembra più un body per neonati o una t-shirt. È una forma costituita da otto aquiloni nel senso geometrico del termine: potete considerarli parenti del rombo (che è un aquilone convesso con tutti e quattro i lati congruenti). Se si disegnano molti esagoni contigui, si può formare “il cappello” prendendo alcuni loro pezzetti con relativa facilità, ma evidentemente fino a Smith nessuno aveva intravisto le potenzialità di quel tassello.

(David Smith et al.)
C’è però un piccolo particolare che non sembra ancora mettere tutti d’accordo sull’einstein di Smith. Il suo tassello permette di raggiungere l’aperiodicità solo se viene utilizzata anche la sua versione speculare nella formazione della tassellazione. Alcuni si sono chiesti se questo dettaglio non faccia sì che in realtà i tasselli siano due e non uno solo, di conseguenza squalificando “il cappello” come einstein. C’è comunque un certo consenso sul fatto che un singolo tassello possa essere considerato tale anche se viene impiegata la sua versione speculare per riempire il piano.
Lo studio di Smith e degli altri autori è stato molto commentato e per ora non sono stati rilevati errori o stranezze, ma la ricerca è comunque in attesa di una revisione formale prima di essere pubblicata su una rivista scientifica. Nel frattempo è già partita la corsa alla ricerca di un einstein che permetta di formare tassellazioni non periodiche senza dover utilizzare anche la sua immagine speculare.