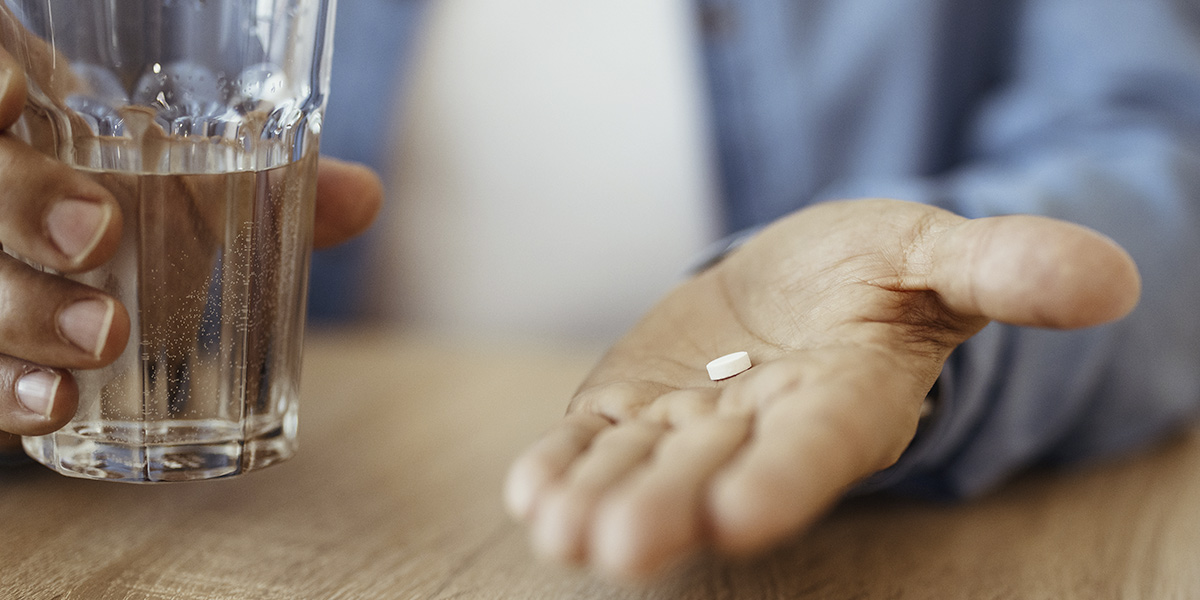
Si fa presto a dire buco

Chiedere a un amico se la cannuccia da cui sta bevendo abbia uno o due buchi può essere un ottimo sistema per rovinargli l’aperitivo. Trovare una risposta che metta d’accordo tutti non è semplice, e si può complicare ulteriormente il dibattito. Il bicchiere che contiene lo Spritz, tecnicamente, ha un buco? E i taralli per accompagnarlo quanti buchi hanno? E le olive, hanno lo stesso problema delle cannucce? In definitiva, che cos’è davvero un buco?

La nostra conoscenza in generale sui buchi è piuttosto lacunosa e la loro definizione ha tenuto a lungo impegnati filosofi, linguisti e matematici. La parola “buco” viene usata per indicare cose piuttosto diverse tra loro, che di solito hanno in comune un’apertura di qualche tipo: il buco della serratura, per esempio. In campo filosofico c’è invece qualche complicazione in più, che deriva dalla difficoltà nel definire i buchi dal punto di vista della loro esistenza.

Prendiamo uno dei taralli dell’aperitivo: se lo mangiamo interamente in un sol boccone, abbiamo mangiato anche il suo buco? La risposta più logica sembra essere sì, ma se invece lo avessimo mangiato gradualmente? In quel caso avremmo spezzato il tarallo, che avrebbe perso il proprio buco, e non lo avremmo mangiato. Questo ci dice che i buchi derivano la loro esistenza e la possibilità stessa di esistere da ciò che hanno intorno.

In un certo senso, e giocando un poco con le parole, i buchi possono essere definiti parassiti: la loro esistenza dipende interamente dall’esistenza di qualcos’altro. Non può esistere un buco se non c’è qualcosa che lo racchiuda.

Nella pratica di tutti i giorni le cose sono più semplici e tutti sanno che cosa sia un buco, quando ne sentono parlare. Gli ingegneri, che sono tipi piuttosto pratici, distinguono tra “buco cieco” e “buco passante”: il primo identifica un’apertura che penetra solo parzialmente un oggetto, mentre il secondo un buco che lo attraversa completamente. Per queste distinzioni preferiscono di solito il termine “foro”, sostanzialmente un sinonimo di buco, ma usato soprattutto per definire qualcosa con margini e ampiezza regolari: un foro nel muro fatto col trapano, per esempio.

Buchi ciechi
Un barattolo di vetro ha un buco cieco: è l’apertura attraverso la quale vi si possono inserire ed estrarre i biscotti. Immaginiamo di poterlo rimodellare, come se fosse di plastilina, e di cambiarne la forma – senza togliere materiale, aggiungerlo o unirlo – fino a fargli assumere quella di un bicchiere. Abbiamo cambiato alcune delle caratteristiche dell’oggetto, ma il buco cieco è rimasto: tecnicamente il bicchiere ha un foro, grazie al quale possiamo riempirlo, vuotarlo e bere.

Ora immaginiamo di poter modellare il bicchiere, allargandolo e riducendone l’altezza, fino a ottenere una scodella. Siamo meno inclini a pensare che una scodella abbia un buco, ma se valeva per il bicchiere, possiamo applicare questa definizione anche in questo caso. La scodella può essere poi modellata in un piatto fondo, che avrebbe ancora un buco cieco per come lo intendiamo, e infine in un piatto piano, che avrebbe invece perso la propria apertura.

In questo ipotetico esperimento, nel passaggio da barattolo a bicchiere a scodella a piatto fondo e infine a piatto piano non abbiamo mai sottratto o aggiunto materiale, né spezzato qualcosa né unito qualcosa insieme (per esempio i margini dell’apertura). Il materiale è rimasto sempre lo stesso ed è stato semplicemente rimodellato: i buchi ciechi possono essere rimossi senza la necessità di chiudere l’apertura che li origina, né di saldarne i margini né di aggiungere altro materiale.

Buchi e topologia
I buchi passanti sono invece più complicati. Il buco di un tarallo pronto per essere infornato non può essere eliminato rimodellandolo nel modo in cui abbiamo cambiato la forma del barattolo di vetro, se non schiacciando e saldando insieme la pasta che costituisce il tarallo, o aggiungendone altra.

Possiamo considerare un tarallo come uno stretto parente della ciambella, che a sua volta è geometricamente definibile come un “toro” (vuoto al suo interno). Per ottenerne uno è sufficiente prendere una circonferenza e farle compiere una rivoluzione intorno a un asse esterno alla stessa.

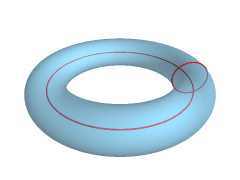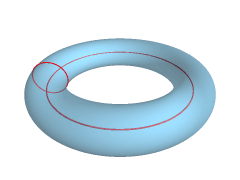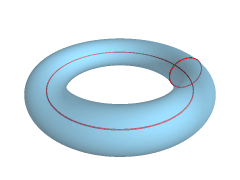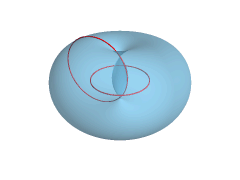
Definire il buco di un toro, e in definitiva un qualsiasi buco passante, richiede un po’ di ginnastica mentale, e tra i più ginnici in questo ambito ci sono i matematici. La loro palestra è la “topologia”, la parte della geometria che si occupa dello studio delle proprietà degli oggetti matematici, che non cambiano quando vengono deformati (a patto di non creare strappi, sovrapposizioni e incollature, come abbiamo visto con gli esempi di prima). Questo modellare senza strappi in topologia viene definito “omeomorfismo”.

In topologia, una sfera e un cubo sono oggetti omeomorfi (cioè equivalenti), perché l’uno può essere deformato nell’altro e viceversa, senza dover aggiungere materiale, o incollarlo o sovrapporlo. Un toro e una sfera non sono invece omeomorfi, proprio perché il toro ha un buco che non può essere in alcun modo eliminato con una semplice deformazione (no, chiudere il buco accostando le parti non sarebbe una semplice deformazione).

Queste condizioni spiegano il modo di dire, a essere onesti diffuso quasi esclusivamente tra chi si occupa di queste cose, secondo cui “i topologi non distinguono una tazza da una ciambella”. I due oggetti sono in effetti omeomorfi: si può ottenere una ciambella partendo da una tazza, semplicemente deformando l’oggetto di partenza senza incollare, creare strappi o sovrapposizioni. I due oggetti sono omeomorfi perché hanno entrambi un solo buco passante (quello cieco della tazza, come abbiamo visto prima, può essere eliminato).

Per i topologi i buchi ciechi non sono particolarmente interessanti, visto che possono essere eliminati, mentre quelli passanti attirano grande interesse, perché hanno caratteristiche uniche e che condizionano il modo in cui possiamo usare le forme geometriche.

Quanti buchi
Tornando all’aperitivo, quanti buchi ha una cannuccia? La domanda era diventata virale su Internet alcuni anni fa, in seguito a un articolo di BuzzFeed sul tema, che aveva ricevuto grandi attenzioni negli Stati Uniti. All’epoca la maggior parte delle persone aveva risposto che i buchi fossero due, riferendosi colloquialmente alle due aperture della cannuccia.

In realtà, una cannuccia e un toro hanno un solo buco. Per rendersene conto è sufficiente immaginare di modellare un toro allungandone la forma, fino a ottenere quella di una cannuccia. Il discorso vale anche al contrario, immaginando di ridurre sempre di più l’altezza della cannuccia, fino a ottenere un toro che avrà al proprio centro un buco.

In termini topologici, una cannuccia può essere descritta come il prodotto tra una circonferenza S¹ e un intervallo I, a sua volta definibile come [0, L] (quindi L definisce la lunghezza della cannuccia). Sul piano geometrico, la circonferenza isola uno spazio che possiamo considerare come un buco, perché l’unico modo per colmarlo sarebbe aggiungendo del materiale o saldando/incollando insieme alcune sue parti. I non ha invece nessun buco, e di conseguenza la cannuccia ha un solo buco.

Partendo da questi elementi di base, che abbiamo semplificato un poco cercando di non bucare i concetti principali, non solo si possono descrivere matematicamente le forme e le loro trasformazioni, ma si possono anche derivare altre informazioni importanti sulle proprietà degli oggetti. L’omologia, per esempio, consente di ricondurre gli oggetti algebrici in successioni di gruppi, che codificano la quantità e il tipo di buchi presenti in ogni oggetto. Taralli compresi.