Le coincidenze capitano

Uno degli aneddoti preferiti sulle coincidenze del matematico Joseph Mazur gli venne raccontato mentre era nel retro di un furgone che saliva tra le montagne della Sardegna. L’autista, un insegnante di italiano chiamato Francesco, gli raccontò del suo incontro con una donna chiamata Manuela, che voleva studiare nella sua scuola. Francesco e Manuela si videro per la prima volta nell’atrio di un albergo, da dove poi andarono a bersi un caffè. Quando venne fuori la scomoda verità stavano chiacchierando da un’ora, per conoscersi. Notando l’italiano quasi perfetto di Manuela, Francesco le chiese come mai aveva deciso di iscriversi alla sua scuola. «”Italiano? Di che parli? Non sono venuta qui per imparare l’italiano”, disse lei», riporta Mazur, «E così entrambi realizzarono che lei era la Manuela sbagliata e lui il Francesco sbagliato». I due ritornarono nell’atrio dell’albergo, dove trovarono un altro Francesco che stava offrendo a un’altra Manuela un lavoro che lei non voleva né si aspettava le venisse offerto. L’aneddoto è una delle molte storie raccontate nel nuovo libro di Mazur, Fluke (“coincidenza”, in italiano), in cui il matematico esplora le probabilità che si verifichino le cosiddette coincidenze.

Mazur sostiene che la maggior parte delle coincidenze della nostra vita – come per esempio incappare in un nostro caro amico dall’altra parte del mondo, conoscere una persona che compie gli anni nel nostro stesso giorno, o addirittura sognare un evento prima che si verifichi – possono essere spiegate con semplici considerazioni matematiche. Se le coincidenze ci sembrano così sorprendenti è perché la maggior parte di noi non sa come funzionano le leggi fondamentali della probabilità.

Le probabilità di incontrare una persona che compia gli anni il nostro stesso giorno

Incontrare una persona con cui condividete il compleanno, per esempio, è una cosa che potrebbe sorprendere. Ma è giusto che sia così? I matematici lo definisco il “problema del compleanno”, e di solito lo formulano in questo modo: quante persone ci vogliono per avere il 50 per cento di probabilità che due di loro compiano gli anni lo stesso giorno? Se è la prima volta che vi imbattete in questo quesito, provate a indovinare prima di continuare a leggere.

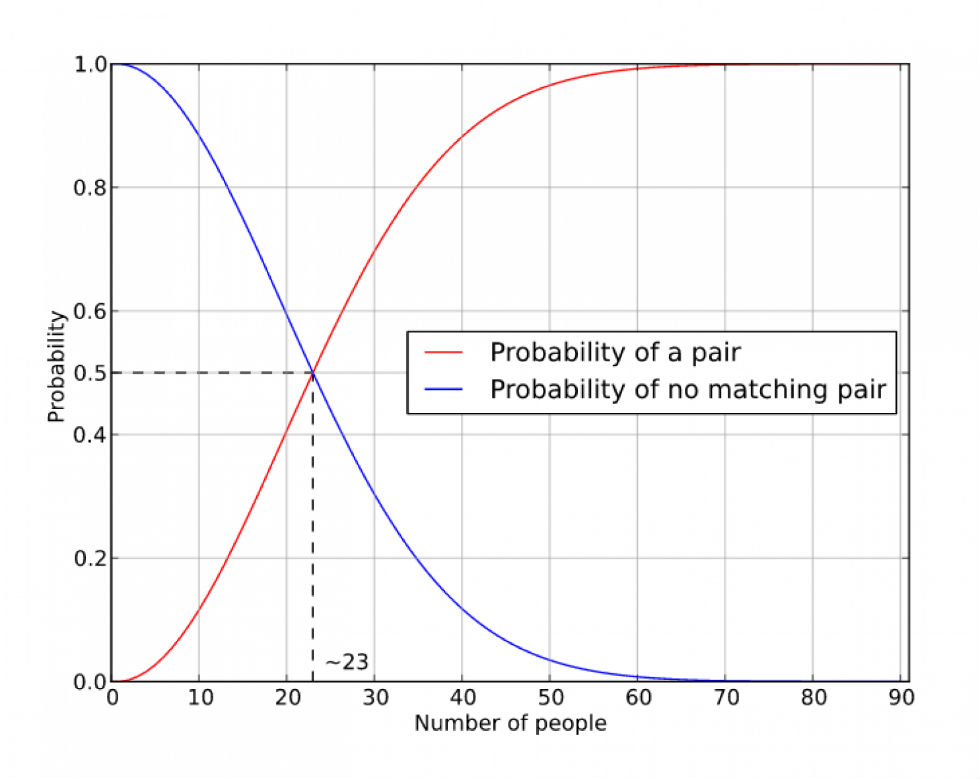
Per cominciare, sapete che se mettete insieme un gruppo di 366 persone c’è il 100 per cento di probabilità che il compleanno di due di loro cada nello stesso giorno, dal momento che in un anno ci sono solo 365 giorni, escludendo gli anni bisestili. Ma si può essere quasi certi che succeda anche con un gruppo di persone molto più piccolo. In questo caso, è più facile considerare il problema opposto, le probabilità cioè di avere in una stanza un gruppo di persone in cui nessuno compia gli anni lo stesso giorno. Per capire quali sono le probabilità che due eventi indipendenti si verifichino insieme – come due persone nate lo stesso giorno – bisogna moltiplicare le probabilità dei singoli eventi.

Le probabilità che il compleanno di due persone non cada lo stesso giorno sono 365/365 x 364/365. Il risultato è circa il 99,7 per cento. Ciò significa che se si considerano due sole persone è molto probabile che il loro compleanno non cada lo stesso giorno. Nel caso di tre persone prese a caso, le probabilità sono del 99,18 per cento. Aggiungendo altre persone all’espressione, però, le probabilità che non ce ne siano due che compiano gli anni lo stesso giorno iniziano a diminuire, prima in modo graduale e poi netto. Con cinque persone, le probabilità sono del 97,3 per cento, mentre con 15 persone diventano del 74,7 per cento. Per ottenere una probabilità superiore al 50 per cento che in una stanza ci siano due persone che compiano gli anni lo stesso giorno bisogna metterne insieme solo 23. Un numero così basso potrebbe sembrare strano, ma considerate che ogni persona che si aggiunge viene confrontata indipendentemente con ogni altro membro del gruppo. Con 23 persone ci sono 253 potenziali accoppiamenti, e quindi ottime probabilità che due di loro abbiano il compleanno in comune. Come mostra il grafico qui sotto, è quasi certo che troverete due persone che compiono gli anni lo stesso giorno prima di arrivare ad averne 60 nel gruppo.

Guillaume Jacquenot (via Wikimedia Commons, CC BY-SA 3.0)

Il problema ha delle interessanti applicazioni pratiche, per esempio se si vuole cercare di capire quante probabilità ci sono che il database del DNA dell’FBI contenga corrispondenze causali tra persone diverse. Nonostante le analisi del DNA che vengono usate per condannare i sospettati nei processi penali siano davvero uniche, alcuni studi hanno dimostrato che le probabilità di trovare una corrispondenza casuale tra due persone non legate tra loro potrebbero essere superiori di quanto pensano le giurie che si esprimono per la colpevolezza di un imputato.

Le probabilità che una scimmia componga un’opera di Shakespeare

Nel suo libro Mazur affronta un altro problema che spiega bene come le persone equivochino il concetto di probabilità: il cosiddetto “problema della scimmia”, formulato dal matematico Emile Borel. Nel 1913 Borel decise di occuparsi di un’annosa questione legata alla casualità, racconta Mazur. «Borel si chiese se degli eventi completamente casuali potevano trasformarsi in un qualcosa che avesse significato, e in breve l’interpretazione popolare della domanda divenne: “Delle scimmie potrebbero comporre un sonetto di Shakespeare digitando a casaccio dei tasti su una tastiera?». La domanda, che probabilmente avete già sentito, si è diffusa nella cultura popolare ed è stata citata anche in una scena dei Simpson nel 1993, in cui Mr. Burns tiene rinchiuse delle scimmie in una stanza costringendole a battere a macchina nella speranza di creare il prossimo capolavoro della letteratura.

Secondo Borel una scimmia alla fine riuscirebbe a comporre un sonetto di Shakespeare, anche se potrebbe volerci moltissimo tempo. Come dice Mazur, la probabilità che una scimmia scriva per caso la parola “posso” – come nel verso “Posso paragonarti a un giorno d’estate?” – è una su quasi 12 milioni. Ma se una scimmia dovesse continuare a provare per molte volte, o se al suo tentativo si unissero altre scimmie, la probabilità inizierebbe a calare. Con 8,2 milioni di tentativi ci sono più possibilità che la scimmia scriva la parola “posso” rispetto al contrario. Lo stesso principio si applica ai tentativi di ottenere una password, in cui degli algoritmi vanno a tentativi per passare in rapida rassegna le potenziali combinazioni. Per questo motivo le password più lunghe sono molto più sicure di quelle brevi, esattamente come per la scimmia è più difficile comporre un intero sonetto rispetto a scrivere solo la parola “posso”.

Perché le coincidenze sono così sorprendenti

Stando a una delle tesi centrali del libro di Mazur, quando pensano alle probabilità le persone tendono a commettere molti errori. Pensate per esempio alle stime basate sulle probabilità come le previsioni sull’esito delle elezioni presidenziali americane fatte dal sito FiveThirtyEight, che nei primi giorni di novembre hanno dato alla candidata Democratica Hillary Clinton il 70 per cento di possibilità di vittoria, contro il 30 per cento del candidato Repubblicano Donald Trump. Guardando l’asimmetria di probabilità come quelle del sito, molte persone danno praticamente per scontata la vittoria di Clinton. Se invece fosse Trump a prevalere, alcune persone potrebbero pensare che FiveThirtyEight si sia sbagliato. Ma ovviamente le probabilità non funzionano in questo modo. Donald Trump ha più di una possibilità su quattro e quindi potrebbe tranquillamente vincere le elezioni di quest’anno.

Un’altra ragione per cui le persone tendono a equivocare le probabilità è la nostra attenzione selettiva: notiamo e ricordiamo le coincidenze, ma difficilmente facciamo attenzione alla loro assenza. Pensate a tutte le persone che avete conosciuto e che non compiono gli anni il vostro stesso giorno, per esempio. È un numero enorme rispetto a quello delle persone il cui compleanno cade insieme al vostro. Dopo aver conosciuto così tante persone che compiono gli anni in un giorno diverso dal vostro, siete destinati a incontrare qualcuno nato il vostro stesso giorno. Questo punto viene illustrato bene dal problema della scimmia: con l’aumentare del numero di tentativi anche gli eventi molto rari hanno un’alta probabilità di verificarsi.

La storia di Francesco e Manuela è un caso simile. Sembra un evento strano, ma se si aggiungono altri abbinamenti di nomi molto comuni e altri atri di alberghi sparsi nel mondo, le probabilità che si verifichi un evento del genere iniziano a crescere. «L’evento dello scambio di identità è più comune di quanto crediamo, perché i numeri dietro questo fenomeno sono più grandi di quello che immaginiamo», scrive Mazur. «Se dovessimo prendere in considerazione tutti gli atri di alberghi di tutto il mondo, i numeri aumenterebbero così tanto che potremmo essere certi del fatto che in qualche atrio di albergo si verificherà uno scambio di identità tra due persone ogni ora».

La tendenza a sovrastimare o sottostimare determinati numeri è la causa della nostra grande sorpresa quando ci troviamo di fronte a una coincidenza. Come scrive Mazur: «A ingannarci spesso è la grandezza del nostro mondo». Vista la quantità di eventi casuali che capitano a così tante persone in giro per il mondo, le coincidenze stupefacenti sono una cosa del tutto naturale.

© 2016 – The Washington Post