Matematica da pausa caffè

Codice edizioni ha pubblicato il libro Matematica in pausa caffè di Maurizio Codogno, matematico e blogger del Post. Il libro, che contiene alcuni degli articoli scritti da Codogno per il blog sul Post insieme ad altri testi mai pubblicati, vuole dimostrare che la matematica non è solo la materia ostile e noiosa che si studia a scuola ma è una parte della vita di tutti i giorni (dalle code nel traffico agli ascensori, da Google ai dadi, dai file troppo compressi alle scommesse) e può essere un buon argomento di conversazione davanti alla macchinetta del caffè.

Il libro sarà presentato giovedì 13 novembre a Roma (ore 18.30 Palazzo delle Esposizioni) e sabato 15 novembre a Milano (ore 11.00, Castello Sforzesco, Portico dell’Elefante, Area Bar: sarà uno degli eventi di BookCity). Di seguito l’introduzione e uno dei capitoli del libro.

***

Il 78,2 per cento degli italiani ritiene che la matematica sia “difficile”. Addirittura il 42 per cento di loro afferma di avere “paura della matematica”. Che dire, di fronte a questi dati? Una cosa è indubbiamente vera: la matematica a livello universitario è difficile. E allora? Anche preparare un cappuccino a regola d’arte non è affatto semplice, e io rimango stupito ogni volta che un barista versa il latte nella tazza e crea il disegno di una foglia o di un cuore. Io non saprei nemmeno da dove iniziare a fare qualcosa del genere: ciò non toglie che possa azionare la mia macchina per il caffè e prepararmi un cappuccino esteticamente non perfetto ma comunque più che onorevole al gusto.

Purtroppo i programmi scolastici impongono che gli studenti ottengano “competenze” che al 99 per cento delle persone non serviranno mai nella vita, e non capita molto spesso la fortuna di trovare un professore davvero bravo, non solo in grado di fare notare che la vita quotidiana è piena di matematica – lo dicono in tanti, e onestamente la cosa inizia a stufare un po’ – ma soprattutto che spieghi come si possano comprendere le idee matematiche anche senza mettersi a fare chissà quali conti. Qualcuno potrà obiettare che se non si fanno conti non è davvero matematica: secondo me è solo una scusa che tirano fuori per continuare a tenersene al largo. Non mi metto a raccontare le solite trite storie su quanto è bella la matematica: io sono assolutamente convinto che lo sia, ma non sono in grado di spiegare perché lo sia. Dico però che ci passano sotto gli occhi tante cose che magari sono difficili da dimostrare in maniera formale, ma si possono capire intuitivamente e raccontare come aneddoti mentre si fanno due chiacchiere alla macchinetta del caffè. In fin dei conti in quei pochi minuti ci capita di parlare di cinema, di economia, di politica, e non è che siamo tutti premi Oscar, Nobel o politici: perché allora non possiamo chiacchierare di temi matematici curiosi?

Questo libro è la raccolta di tanti piccoli argomenti, tutti trattati in tre o quattro pagine e pensati come se fossero da raccontare a chi matematico non è. Sì, a volte ci sono degli esempi numerici, ma garantisco che potete fidarvi del risultato. C’è anche qualche figura, ma non troppe, perché un disegnino da solo serve davvero a poco nonostante quello che si sente dire: se poi trovate qualche formula, garantisco che l’ho inserita solo per il suo valore estetico, e anche se la saltate a piè pari non succederà nulla. Non penserete mica di fare i disegnini o scrivere formule usando la palettina fornita dalla macchinetta e la schiuma del cappuccino?

Nel testo troverete cinque sezioni. Aritmetica ha le risposte ad alcune domande che probabilmente vi siete posti ai tempi della scuola e poi avete dimenticato; Paradossi, probabilità, previsioni raccoglie problemi che a prima vista sembrano impossibili ma a un esame più attento risultano del tutto logici; Giochi… beh, come dice il titolo, tratta di giochi, di azzardo e non; Andando in giro tratta esempi che si possono trovare quando ci si muove per strada e altrove; infine Computer e standard tratta questioni un po’ meno legate alla matematica, anche se c’è chi è convinto che l’informatica non sia altro che matematica sotto mentite spoglie. Ciascun capitoletto può essere letto da solo, anche se a volte ci sono dei richiami ad altri capitoli in cui un certo tema è trattato in modo un po’ diverso; alcuni degli argomenti vi saranno forse noti, ma spero che anche in quel caso saprò trattarli in modo diverso da quello che conoscevate. Oltre a farvi divertire con le curiosità che racconto nel libro, cercherò di far comprendere in modo intuitivo cosa c’è davvero sotto: appartengo alla scuola che ritiene che scopo della matematica sia fondamentalmente creare modelli che poi verranno più o meno perfettamente applicati alla realtà, e la vera sfida sia riuscire a farsi un’idea della struttura logico-matematica di quello che ci circonda. Saper risolvere equazioni o calcolare integrali non ci serve a molto nella vita di tutti i giorni, e se proprio ci serve possiamo sempre prendere un computer e dargli in pasto la formula.

Se però non abbiamo un’idea qualitativa di cosa dobbiamo aspettarci, corriamo davvero il rischio che qualcuno sfrutti una massa di numeri e formule piazzati più o meno a caso per propagare una bufala, sfruttando l’innumeratezza (l’analfabetismo numerico) della gente. È da fine 2012 che circola su Facebook e altrove questo testo: «Ieri il Senato della repubblica ha approvato con 257 voti favorevoli e 165 astenuti il disegno di legge del Senatore Cirenga che prevede la nascita del fondo per i “parlamentari in crisi” creato in vista dell’imminente fine legislatura. Questo fondo prevede lo stanziamento di 134 miliardi di euro da destinarsi a tutti i deputati che non troveranno lavoro nell’anno successivo alla fine del mandato». Quanti di quelli che l’hanno letto e condiviso non hanno nemmeno sommato il numero di voti indicati, per accorgersi che erano più dei membri del Senato, o diviso la somma stanziata per i meno di mille parlamentari, per scoprire che ciascuno di essi avrebbe ottenuto più di 130 milioni? Di matematica ne serviva poca, di buon senso non molto di più: se la prima non vi spaventerà, sono certo che del secondo ne avete più che a sufficienza.

Ah, dimenticavo: le statistiche che ho riportato all’inizio me le sono inventate sul momento. Per favore non condividetele su Facebook…

I miei amici hanno più amici di me
Una tavola dei Peanuts aveva come ambientazione una festa di san Valentino. I bambini arrivavano con un maz­zetto di Valentines (cartoline di auguri che negli Stati Uniti non si danno solo al proprio fidanzato o fidanzata, ma si scambiano anche tra amici). Alla fine della festa tutti tor­nano a casa con un mazzetto di Valentines ricevute… tran­ne Charlie Brown, che resta sconsolatamente a mani vuote.

D’accordo, direte: Charlie Brown non viene mai considera­to, e nessuno si stupisce nel vedere che tutti gli altri hanno più amici di lui. All’atto pratico, però, la maggior parte di noi è Charlie Brown. Di amici ne abbiamo, sì, ma i nostri amici hanno generalmente, in media, più amici di quanti ne abbiamo noi. Questa affermazione, tra lo scioglilingua e il paradosso, è stata dimostrata empiricamente: nel maggio 2011 due dottorandi, Johan Ugander e Brian Karrer, hanno avuto a disposizione l’intera struttura di Facebook – al tem­po gli utenti erano solo 721 milioni – e controllando la rete di amicizie hanno scoperto come nel 93 per cento dei casi la media delle amicizie dei nostri amici era maggiore del nu­mero dei nostri amici. In media un utente aveva 190 amici, mentre i suoi amici in media ne avevano più del triplo, per la precisione 635. Complotto? Dati fasulli? Come sempre la risposta è molto più semplice; ma è meglio prendere le cose più alla lontana.

Iniziamo con un esempio di tutt’altro tipo. Io mi dedico coscienziosamente alla pesistica, giusto per mantenere un minimo di forma fisica: non sono certo Mister Muscolo, ma credo di essere nella media. Eppure, a qualunque ora io entri in palestra, mi sembra sempre di essere circondato da culturisti. Non che mi preoccupi più di tanto, intendiamoci: però a prima vista la cosa è sconcertante.

Quale può essere la causa di una simile anomalia? Beh, un palestrato, come dice il nome stesso, passa molto più tempo in palestra di una persona normale; quindi è molto più probabile incon­trare un culturista rispetto a un utente qualunque, e dunque la percentuale percepita di uomini molto muscolosi è mag­giore di quella attuale ricavabile controllando i dati degli iscritti alla palestra.

Un secondo esempio: immaginate di essere un insegnan­te, e di tenere due corsi. Il primo corso è introduttivo e ha 90 studenti, mentre il secondo è un seminario di perfezio­namento con solo 10 iscritti. Considerazioni didattiche a parte, è evidente che in media avete 50 studenti per classe.

Guardiamo però la cosa dal punto di vista degli studenti: per 90 di loro la classe è formata da 90 studenti e per gli altri 10 è formata da 10. In media abbiamo così (90×90 + 10×10)/(90+10) studenti, quindi in media ci sono 82 stu­denti per classe. Ancora una volta c’è qualcosa che non va. Il pattern dovrebbe però essere più chiaro: la differenza è tra uno sguardo oggettivo (contare le tessere e gli studenti) e uno soggettivo (i proprio compagni). Quando c’è una di­suguaglianza tra gli insiemi di riferimento – i frequentatori casuali di una palestra che ci stanno poco e quelli abituali che sono sempre là; gli studenti di una classe affollata e quelli di un seminario per pochi intimi – e si calcola la me­dia usando come riferimento ciascun elemento dell’insieme, chi ha tante connessioni conta molto di più e distorce la me­dia complessiva. Proviamo ora a fare i conti con un insieme minuscolo, come quello della figura qui sotto.

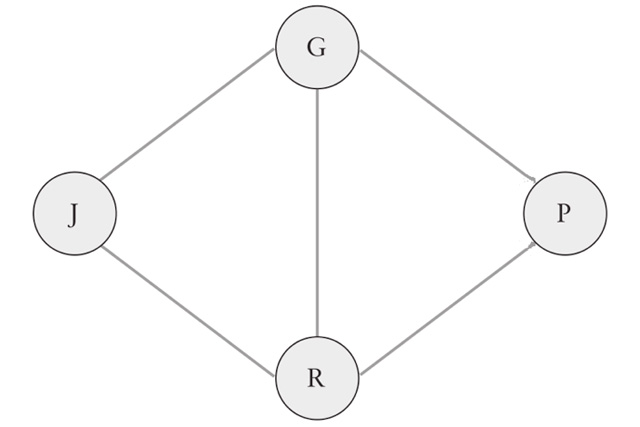
Eravamo quattro amici a Liverpool

I cerchi rappresentano persone; i segmenti che li congiungono, relazioni di amicizia. Facendo la somma degli amici di ciascuno, si arriva a 2+3+3+2 = 10 amicizie (ogni relazione è contata 2 volte) per 4 persone, quindi una media di 2,5 amici a testa. Vediamo ora la media degli “amici degli amici”.

Lo scioglilingua si traduce in questo modo: per ogni persona consideriamo i suoi amici, per ciascuno di loro i suoi amici, e infine facciamo la media. John ha 2 amici, George e Ringo, che hanno 3 amici ciascuno; lo stesso vale per Paul. I loro amici hanno quindi in media 3 amici. George e Ringo hanno invece 3 amici: 2 (John e Paul) che hanno a loro volta 2 amici, e 1 con 3 amici; la media di amici per amico è 7/3. La media complessiva, dunque, è 8/3, un valore leggermente superiore a quello calcolato prima. Più la struttura delle amicizie è sparsa, maggiore risulterà la differenza tra il numero medio di amici. Se aggiungiamo al grafo delle amicizie Eleanor, che ha come unico amico Ringo (chi non è amico di Ringo?), il numero totale di amicizie diventa 12, e la media scende a 2,4 amici. Gli amici, però, hanno in media circa 3,13 amici ciascuno: più di prima! Con i dati di Facebook capita appunto qualcosa di simile.

Attenzione, però! Questo apparente paradosso funziona con Facebook, ma se fate la stessa cosa con i seguaci di Twitter otterrete risultati completamente diversi. Infatti seguire qualcuno non è un’azione simmetrica: A può seguire B, ma magari B non ha neppure idea che A esista. Quindi il fattore moltiplicativo che abbiamo visto nell’esempio delle due classi – tutti gli studenti di una classe hanno tutti gli altri studenti come compagni – non vale più. Insomma, Twitter non è un Facebook con gli status più brevi, ma c’è proprio (almeno) una differenza di fondo.