Come te la caveresti in terza media?

Giovedì 19 giugno gli studenti che hanno terminato la terza media, il terzo anno della scuola secondaria di primo grado per fare quelli puntigliosi, si sono dati da fare per rispondere alle domande di italiano e di matematica delle prove INVALSI. L’Istituto Nazionale per la Valutazione del Sistema Educativo di Istruzione e Formazione (INVALSI per l’appunto) è l’ente che si occupa di valutare la qualità della scuola italiana e capire entro certi limiti le cose che non vanno. Le prove sono una serie di test, dalla comprensione del testo alla risoluzione di problemi, che sono poi corretti dagli insegnanti di ogni scuola. L’INVALSI riceve i risultati da tutti gli istituti scolastici italiani e sulla base di questi prepara classifiche e statistiche.

Qui sul Post da ormai cinque anni (uno, due, tre, quattro, questo è il quinto) selezioniamo e vi proponiamo alcuni dei test delle prove INVALSI. E la domanda rimane e continuerà a essere sempre la stessa: come ce la caveremmo oggi, in terza media?

Per leggere le risposte, selezionare col puntatore il testo dopo “Risposta:”: è scritto in bianco.

ITALIANO

1. Nella frase “Secondo una prima ricostruzione, il ladro sarebbe entrato da una finestra sul retro”, il verbo indica:

a. un’azione certa;
b. un’azione futura.
c. un’azione improbabile.
d. un’azione possibile.

Risposta: d.

 

2. “Raggiunta la cima, il gruppo degli alpinisti decise di trascorrere la notte nel rifugio”. La frase in grassetto è:

a. consecutiva;
b. temporale;
c. finale;
d. concessiva.

Risposta: b.

 

3. Indica in quali dei seguenti aggettivi “in-“ è un prefisso con valore negativo:

a. indeciso;
b. intenso;
c. innamorato;
d. interno;
e. incapace;
f. integrale;
g. incivile;
h. insolubile.

Risposta: a, e, g, h.

 

4. In quale delle seguenti frasi è presente una espressione polirematica (cioè un gruppo di più parole con un significato unitario).

a. Quella ragazza ha un viso acqua e sapone.
b. Per la cena di stasera mancano pane e vino.
c. Nella fattoria razzolavano liberamente galli e galline.
d. Sbuccia la frutta con forchetta e coltello!

Risposta: a.

 

5. “Luca mi ha chiesto quando arriverà l’aereo da Milano”, la parte in grassetto è una frase:

a. soggettiva;
b. oggettiva esplicita;
c. temporale;
d. interrogativa indiretta.

Risposta: d.

 

6. Nella frase “Era previsto uno spettacolo magnifico, ma a causa del maltempo fu annullato: quando lo seppi ci rimasi male” lo a che cosa si riferisce:

a. al fatto che lo spettacolo fu annullato;
b. al maltempo;
c. al fatto che era previsto uno spettacolo magnifico;
d. allo spettacolo.

Risposta: a.

 

7. Indica i modi dei verbi della frase “Avendo visto in vetrina un bellissimo maglione ho deciso di comprarlo, benché fosse molto caro”.

a. Gerundio, indicativo, participio, congiuntivo.
b. Gerundio, participio, indicativo, infinito.
c. Gerundio, indicativo, infinito, congiuntivo.
d. Gerundio, indicativo, infinito, condizionale.

Risposta: c.

 

8. Nella frase “Inviterò anche Maria perché tu la conosca” la congiunzione “perché” ha valore:

a. casuale;
b. interrogativo;
c. finale;
d. consecutivo.

Risposta: c.

Tenetevi pronti, nella prossima pagina si inizia con la matematica.

MATEMATICA

1. Una fabbrica produce 1000 lampadine, di cui 30 difettose. Ne vende 100 e tra queste 12 risultano difettose. Se si scegli a caso una lampadina tra quelle rimaste da vendere, qual è la probabilità che sia difettosa?

a. 18/900
b. 108/900
c. 30/1000
d. 120/1000

Risposta: a.

 

2. La famiglia Rossi, composta da due adulti e due bambini di 3 e 5 anni, deve noleggiare un’automobile per una settimana. Cerca su Internet e trova le seguenti offerte.

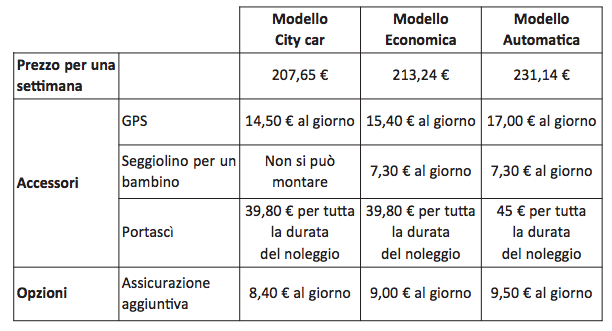
a. La famiglia Rossi decide di noleggiare un’automobile Modello Economica con GPS e seggiolini per i bambini. Indica i prezzi nella tabella che permettono di calcolare la spesa della famiglia Rossi per il noleggio dell’automobile.
b. Quanto spende la famiglia Rossi per il noleggio dei seggiolini?

Risposta: a. 213,24 – 15,40 – 7,30 / b. 102,20.

 

3. Una scatola a forma di parallelepipedo ha quattro facce rettangolari uguali di dimensioni 6 cm e 10 cm. Indica se ciascuna delle seguenti affermazioni è vera o falsa.

a. Le altre due facce possono essere due quadrati di 6 x 6 cm.
b. Le altre due facce possono essere un quadrato di 6 x 6 cm e un rettangolo di 6 cm x 10 cm.
c. Le altre due facce possono essere un quadrato di 10 x 10 cm e un rettangolo di 6 x 10 cm.
d. Le altre due facce possono essere due quadrati di 10 x 10 cm.

Risposta: a. Vero; b. Falso; c. Falso; d. Vero.

 

4. Due candele di cera, alte entrambe 30 cm, vengono messe in un portacandela in posizione verticale e accese.

La candela A si accorcia di 0,5 cm ogni 3 minuti mentre la candela B si accorcia di 0,5 cm ogni minuto.

A. Dopo 10 minuti di quanto si saranno accorciate le due candele?

a. Candela A: circa 1,6 cm; Candela B: 5 cm.
b. Candela A: circa 3 cm; Candela B: 1 cm.
c. Candela A: circa 15 cm; Candela B: 10 cm.
d. Candela A: circa 9 cm; Candela B: 10 cm.

B. Quale delle seguenti formule esprime l’altezza L in centimetri della candela B al variare del numero n di minuti?

a. L = 30 – 3 • n
b. L = 30 – 1,5 • n
c. L = 30 – n
d. L = 30 – 0,5 • n

Risposta: A. a; B. d.

 

5. La seguente figura rappresenta il prato davanti alla casa di Paolo.

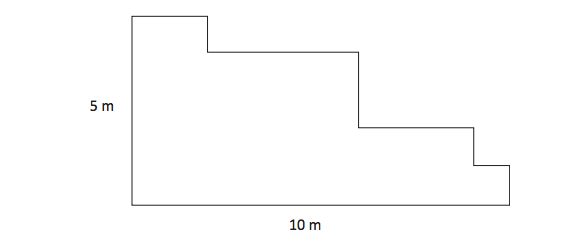
È possibile, con i dati a disposizione, calcolare il perimetro del prato?

a. Sì, misura 15 m.
b. Sì, misura 30 m.
c. Sì, misura 50 m.
d. No, non si può calcolare.

Risposta: b.

Nella prossima, si sale in treno, circa.

6. Due treni viaggiano uno verso l’altro con velocità costanti. Individua tra i seguenti grafici quello che descrive come varia la distanza tra i due treni al passare del tempo.

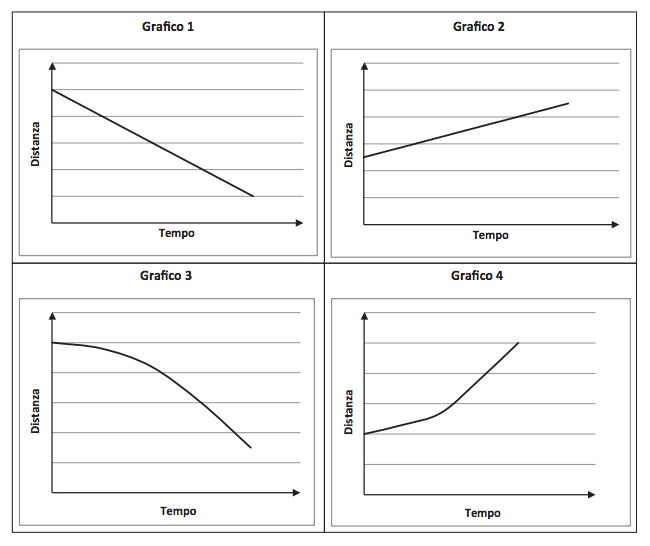
Risposta: Grafico 1.

 

7. Nella pizzeria “Da Marco” la pizza margherita costa 5 euro. Il mercoledì, però, per chi compra più pizze, c’è un’offerta speciale. Il seguente grafico rappresenta come varia, il mercoledì, la spesa complessiva, in euro, al variare del numero delle pizze margherita acquistate.

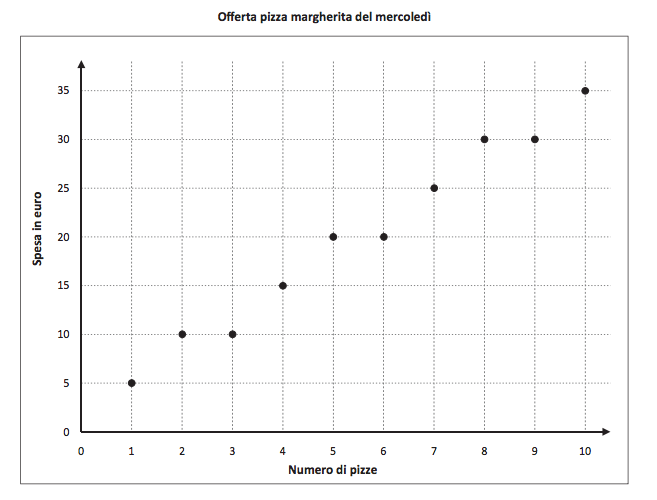
Indica se ciascuna delle seguenti affermazioni è vera o falsa.

a. Il mercoledì, il risparmio rispetto agli altri giorni, in percentuale, è sempre lo stesso qualunque sia il numero di pizze acquistate.
b. Il mercoledì, una pizza su tre è gratis.
c. Il mercoledì, se si comprano 4 pizze, il risparmio rispetto agli altri giorni è del 25 per cento.

Risposta: 1. Falso; 2. Vero; 3. Vero.

 

8. Osserva i triangoli nella seguente figura.

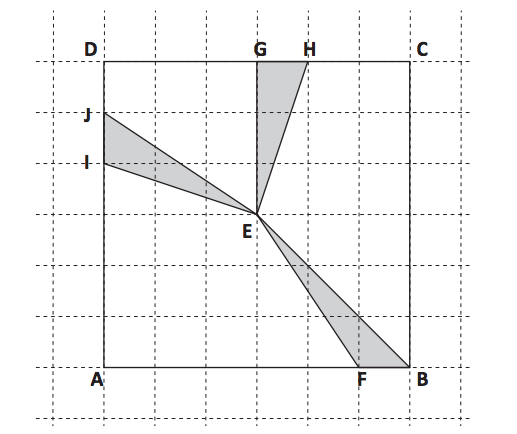
A. Quale delle seguenti affermazioni è corretta?

a. I tre triangoli hanno la stessa area e stesso perimetro.
b. I tre triangoli hanno stessa area e diverso perimetro.
c. I tre triangoli hanno diversa area e stesso perimetro.
d. I tre triangoli hanno diversa area e diverso perimetro.

B. Dove va posizionato sul lato AB del quadrato il punto P in modo che il triangolo AEP abbia area doppia del triangolo EFB?

Risposta: A. b; B. Dopo il secondo quadretto da sinistra.

 

9. A un torneo di tennis, uno contro uno, partecipano 16 giocatori. Il torneo si svolge a eliminazione diretta, cioè chi perde una partita viene eliminato. Qual è il numero di partite necessario per stabilire il vincitore del torneo?

a. 8.
b. 15.
c. 16.
d. 32.

Risposta: b.

 

10. Una scuola ha dieci classi, con una media di 22 alunni per classe. Le classi con 21 alunni sono sei; le classi con 24 alunni sono tre. Quanti alunni ci sono nella decima classe?

a. 20.
b. 22.
c. 23.
d. 25.

Risposta: b.

11. Osserva il grafico.

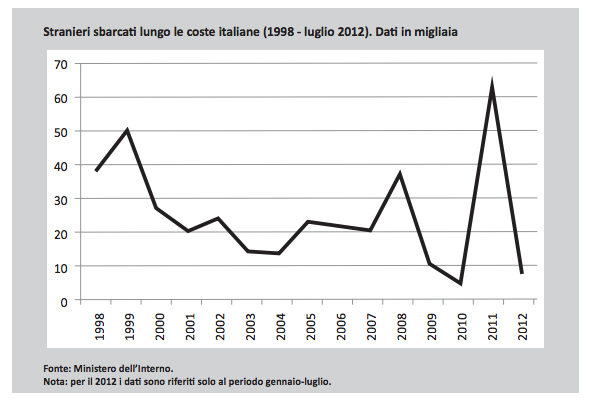
Indica se ciascuna delle seguenti affermazioni è vera o falsa.

a. Nel 1999 sono sbarcati circa 50 stranieri.
b. Il 2010 è stato l’anno in cui sono sbarcati meno stranieri.
c. Dal 1999 al 2004 il numero di stranieri sbarcati è andato sempre diminuendo.
d. Nel 2011 il numero di stranieri sbarcati è stato circa 6 volte quello degli stranieri sbarcati nel 2009.

Risposta: a. Falso; b. Vero; c. Falso; d. Vero.

Forza, è quasi finita e potete ancora dare il meglio.

12. In Italia, secondo gli ultimi dati forniti dall’ISTAT, ci sono circa 600 automobili ogni 1000 abitanti. Gli abitanti dell’Italia sono circa 60 milioni e un’automobile è lunga mediamente 4 metri. Immagina di posizionare tutte le automobili che ci sono in Italia una dietro l’altra, formando un’unica fila continua: quanti chilometri sarebbe all’incirca lunga questa fila?

a. Sarebbe all’incirca lunga come l’Italia (circa 1000 km).
b. Sarebbe all’incirca lunga come la distanza tra l’Italia e gli USA (circa 6000 km).
c. Sarebbe all’incirca lunga come l’equatore (circa 40000 km).
d. Sarebbe all’incirca lunga come il diametro del pianeta Giove (circa 143000 km).

Risposta: d.

13. Leonardo vuole costruire una mensola. La parte sporgente delle assi della mensola è di lunghezza uguale a quella del lato del quadrato centrale. Qui sotto è riportato lo schema della parte posteriore della mensola con le misure. Affinché la mensola sostenga il peso dei libri è necessario mettere una sbarretta d’acciaio che colleghi il punto A con il punto B come nello schema.

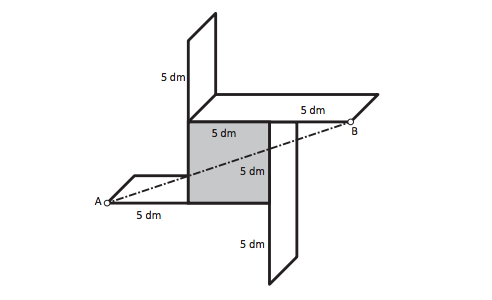
Quanto deve essere lunga la sbarretta?

a. Circa 11 dm.
b. Circa 16 dm.
c. Circa 20 dm.
d. Circa 25 dm.

Risposta: b.

 

14. Luisa non si ricorda bene la combinazione del lucchetto della sua bicicletta. La combinazione si ottiene girando quattro rotelline, ognuna delle quali riporta tutte le cifre da 0 a 9. Luisa non ricorda per nulla la seconda cifra della combinazione, ma sa che: la prima cifra è 6; la terza cifra è 3 o 4; l’ultima cifra è 1. Quante combinazioni al massimo dovrà provare Luisa per riuscire ad aprire il lucchetto della sua bicicletta?

a. 2.
b. 3.
c. 10.
d. 20.

Risposta: d.

 

15. Nel triangolo in figura il segmento AM congiunge il vertice A con il punto medio M del lato BC. Il triangolo risulta così diviso in due triangoli.

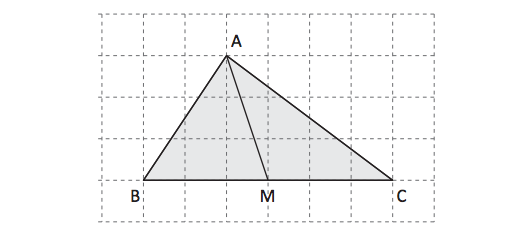
I due triangolo ABM e AMC risultano tra loro equivalenti?

a. Sì, perché i triangoli ABM e AMC hanno una base e la relativa altezza di uguali lunghezze.
b. Sì, perché il lato AM è in comune ai triangoli ABM e AMC.
c. No, perché i triangoli ABM e AMC non sono congruenti.
d. No, perché il segmento AM è la mediana relativa al lato BC del triangolo ABC.

Risposta: a.

 

16. Osserva la figura.

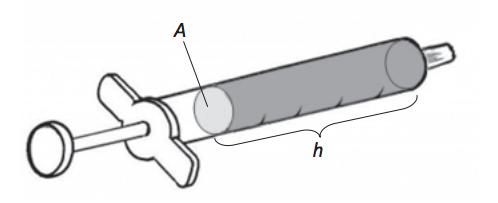
A. La lunghezza della colonna del liquido contenuto nella siringa è indicata con h. Il volume del liquido è V. Indica la formula che ti permette di calcolare l’area A della sezione della siringa conoscendo h e V.

B. Lo stesso volume V di liquido viene messo in una seconda siringa e la lunghezza della colonna di liquido diventa il doppio. L’area della sezione di questa siringa rispetto alla prima è:

a. il doppio;
b. un quarto;
c. la metà;
d. il quadruplo.

Risposta: A. V/h; B. c.

 

17. Considera la frazione 400/500. Indica se ciascuna delle seguenti affermazioni è vera o falsa.

a. Aggiungo 1 al numeratore: 401/500 è maggiore di 400/500;
b. Aggiungo 1 al denominatore: 400/501 è minore di 400/500.
c. Aggiungo 1 sia al numeratore sia al denominatore: 401/501 è equivalente a 400/500.
d. Sottraggo 1 sia al numeratore sia al denominatore: 399/499 è equivalente a 400/500.

Risposta: a. Vero; b. Vero; c. Falso; d. Falso.