Quattro regole per criticare con gentilezza

Gli esseri umani sono per natura buoni o cattivi? Il genere umano si interroga su questa domanda più o meno da sempre: già un paio di secoli prima della nascita di Gesù Cristo – che avrebbe detto chiaramente cosa era giusto, ma meno chiaramente cosa era “naturale” – i pensatori latini si interrogavano su quale fosse l’attitudine innata degli esseri umani. Già il commediografo Tito Maccio Plauto, nell’Asinaria, riporta un parere dell’epoca sulla questione, forse una specie di proverbio: lupus est homo homini, cioè gli uomini sono come lupi per gli altri uomini. Il filosofo Lucio Anneo Seneca pensava il contrario e scrisse che “gli uomini sono sacri per gli altri uomini”.

A differenze di molte delle altre grandi domande che i filosofi si sono posti nel corso dei secoli, la questione della bontà degli esseri umani ha un risvolto pratico e applicabile nella vita di tutti i giorni. In un mondo di “buoni” è conveniente essere disponibili nei confronti degli altri. In un mondo di lupi, invece, è molto meglio girare armati di un grosso bastone. Il filosofo americano Daniel Dennett, che si occupa da molti anni dello studio del funzionamento della mente umana, ha scritto nel suo ultimo libro, “Strumenti per pensare” (uscirà in Italia ad aprile per l’editore Cortina) che in un certo senso ha ragione Seneca: è più utile essere buoni.

In un capitolo del libro arriva a sostenere l’importanza di essere gentili anche in una delle attività umane dove in genere (soprattutto davanti a un pubblico e soprattutto in televisione) consideriamo spregiudicatezza e aggressività doti piuttosto essenziali per ottenere la vittoria: la discussione. Secondo Dennett, per vincere in una discussione, invece, è utile seguire “quattro semplici regole per criticare con gentilezza”:

1. Cerca di ripetere l’affermazione del tuo avversario in maniera così chiara, vivida e onesta che lui non possa risponderti altro che “grazie, vorrei averlo detto in questo modo”

2. Elenca ogni punto sul quale siete d’accordo, specialmente se non sono cose banali e su cui non c’è un accordo universale

3. Menziona tutto quello che hai imparato dal discorso del tuo avversario

4. Solo a questo punto ritieniti autorizzato a confutare o criticare quello che ha detto il tuo avversario

L’effetto di questa strategia, scrive Dennett:

[…] il tuo avversario sarà più ricettivo nei confronti delle critiche: gli hai fatto capire che comprendi quanto lui stesso le sue posizioni e gli hai dimostrato di essere giudizioso (sei d’accordo con lui su alcuni argomenti importanti e sei stato persuaso da qualcosa che lui ha detto). […] A volte, quando non è coronata dal successo, l’eroica ricerca di qualcosa da difendere nel ragionamento di qualcuno è più devastante di una critica fatta con l’accetta.

Dennett scrive che il primo ad avergli dato l’idea delle quattro regole è stato lo psicologo e matematico Anatole Rapaport, uno dei principali studiosi della teoria dei giochi e del principio della cooperazione. Rapaport contribuì a dare una risposta all’antica domanda dei filosofi dal punto di vista scientifico e biologico. Con l’aiuto di altri scienziati riuscì a dimostrare che l’altruismo è conveniente e che nella lotta per la sopravvivenza in natura i buoni arrivano primi e ci riuscì anche grazie a uno degli esperimenti più affascinanti e replicati degli ultimi cinquant’anni: “il torneo di Axelrod”.

Il dilemma del prigioniero
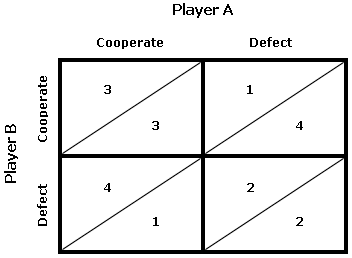
Nel 1981 il sociologo Robert Axelrod organizzò un torneo di un “gioco” chiamato “il dilemma del prigioniero”. Si tratta di un esperimento molto semplice, inventato negli anni Cinquanta, per provare a dare una risposta scientifica a una domanda molto vicina a quella da cui siamo partiti: ci conviene essere buoni o cattivi quando trattiamo con gli altri esseri umani? Il dilemma del prigioniero funziona in questo modo: due giocatori interpretano due ladri arrestati dalla polizia. Sono tenuti in due celle diverse e non hanno possibilità di comunicare. Ognuno dei due ha a disposizione due scelte: può denunciare il proprio complice (un’opzione che chiameremo “tradire”) oppure tacere (una mossa che chiameremo “cooperare”). Se entrambi tacciono la polizia si ritrova senza prove ed è costretta a liberarli dopo qualche settimana. Se uno dei due tace (coopera) mentre l’altro lo denuncia (tradisce), il primo finisce in prigione per un lungo periodo mentre l’altro viene liberato. Se invece entrambi si accusano (entrambi giocando “tradimento”), il giudice considera le loro testimonianze poco affidabili e li condanna entrambi a un periodo medio di carcere. Lo scopo del gioco è cercare di “rimanere in carcere” il meno possibile.

Lo schema qui sopra sintetizza le scelte dei due giocatori e i “punteggi” che possono ottenere. Abbiamo detto che i giocatori hanno a disposizione solo due mosse. Se giocano entrambi “cooperazione” ottengono un punteggio medio (casella in alto a sinistra), se entrambi tradiscono ottengono un punteggio basso (casella in basso a destra). Se uno tradisce mentre l’altro coopera, ottiene il massimo del punteggio, mentre l’altro ottiene il minimo (le altre due caselle). Nel dilemma del prigioniero la mossa migliore è quasi sempre giocare “tradimento”. In questo modo se il nostro avversario gioca “cooperazione” otteniamo una vittoria netta, mentre se l’altro “tradisce” a sua volta avremo ottenuto comunque un pareggio.

Axelrod però non era interessato a questa versione semplice del dilemma: voleva scoprire quale fosse la strategia migliore in una serie reiterata di dilemmi del prigioniero. In questa versione del gioco, due giocatori si affrontano in diverse partite del dilemma del prigioniero alla fine delle quali si sommano i punti e si guarda chi ha vinto. Per complicare le cose, Axelrod decise che i suoi giocatori avrebbero giocato diversi incontri gli uni contro gli altri e poi – come in un campionato di calcio – avrebbero giocato a turno contro tutti gli altri partecipanti al torneo. Lo scopo di Axelrod non era studiare come reagissero i singoli giocatori messi davanti alla scelta tra cooperazione e tradimento: voleva scoprire quale fosse la strategia migliore da adottare in situazioni simili, quella che assicurasse il punteggio più alto in una lunga serie di partite. Per questo motivo, chiese ad amici, colleghi e altri ricercatori di elaborare dei programmi informatici che simulassero il comportamento di un giocatore, con l’obiettivo di massimizzare il punteggio. Ciascuno avrebbe scelto una strategia diversa e Axelrod avrebbe potuto valutare l’efficacia di ciascuna facendo giocare ripetutamente i programmi gli uni contro gli altri. Al torneo parteciparono quindici programmi ed ogni partita era costituita da duecento manche consecutive di dilemma del prigioniero. Dopo essersi scontrato contro tutti gli avversari, ogni programma avrebbe giocato un’ultima serie di partite contro una copia di sé stesso.

Molti dei programmi inviati ad Axelrod si basavano su strategie molto complesse che occupavano decine e decine di righe di codice. Molte di queste strategie erano “cattive”, nel senso che si basavano sul principio che nel dilemma del prigioniero giocato una volta sola, la cosa che conviene fare è tradire sempre. Piuttosto a sorpresa, invece, Axelrod scoprì che a vincere fu la strategia più semplice di tutte e una delle più “buone” (cioè che non cercava di “fregare” gli altri programmi). Si chiamava “Tit for tat” (che significa più o meno “occhio per occhio”) e occupava appena quattro righe di BASIC (un codice di programmazione). Le sue istruzioni dicevano più o meno così: come prima mossa coopera sempre, dopodiché copia quello che fa il tuo avversario: se coopera rispondi cooperando, se tradisce rispondi tradendo. L’autore di questa strategia semplice e geniale era uno scienziato che aveva molta fiducia nella capacità dei comportamenti altruistici di prevalere su quelli egoistici: Anatole Rapaport, cioè l’autore delle quattro regole per criticare con gentilezza.

Come faceva il semplice e “buono” Tit for Tat a battere i suoi astuti e crudeli avversari? Più o meno andava così: immaginiamo uno scontro tra Tit for Tat e un programma chiamato “Tradisci sempre”. La prima mano Tit for Tat viene “fregato”, e “Tradisci sempre” fa il massimo dei punti. Dalla mano successiva, però, Tit fot Tat risponde con un tradimento ed entrambi fanno pochissimi punti. Quando “Tradisci sempre” incontra la copia di sé stesso le cose gli vanno peggio: tradimento su tradimento, finisce con ottenere quasi il minimo dei punti. Quando Tit for tat incontra sé stesso invece coopera continuamente, ottenendo un punteggio molto superiore. Per quanto fossero complessi i programmi “cattivi”, il loro torneo finiva sempre in modo simile: i “cattivi” battevano Tit for tat nell’uno contro uno, ma ottenevano sempre pessimi punteggi quando incontravano gli altri programmi cattivi e le copie di sé stessi. Tit for tat perdeva gli scontri con i “cattivi”, ma vinceva contro sé stesso e contro gli altri programmi “buoni”, totalizzando più punti (se avete già notato che qualcosa non torna, non preoccupatevi: ci torneremo tra poco).

In realtà c’era un concorrente ancora migliore di Tit for Tat. Non partecipò al torneo, ma Axelrod lo inserì successivamente in un’altra serie di simulazioni. Si chiamava Tit for two tats. Funzionava come il suo parente, ma dava una “possibilità” in più al suo avversario. Dopo il primo tradimento, Tit for two tats continuava a cooperare e tradiva solo al secondo tradimento del suo avversario. Nelle simulazioni con i 15 programmi originali Tit for two tats ottenne sistematicamente punteggi migliori di Tit for tat. Questo perché la sua strategia “ancora più buona” evitava di farlo finire in spirali di ritorsioni. Per esempio, Tit for two tats funzionava meglio negli incontri con un programma di nome “Random”. Questo programma giocava sempre cooperazione, ma ogni tanto, in maniera del tutto casuale, giocava un tradimento, dopo di ché cominciava a copiare l’ultima mossa del suo avversario. Il tradimento innescava a sua volta un tradimento di Tit for tat, che portava a una spirale di rappresaglie. Tit for two tats, invece, lasciava correre il primo tradimento: “Random” tornava a cooperare e il gioco finiva con un punteggio più alto per entrambi. Sembrava incredibile: la strategia più ingenua era anche la migliore.

Tre anni dopo, nel 1984, dopo un secondo torneo a cui parteciparono 63 programmi, Axelrod scoprì che Tit for two tats era andato molto peggio del suo cugino più severo. Cosa era accaduto? Con molti più programmi in gara, Tit for two tats si era trovato davanti avversari molto più pronti a sfruttare la sua generosità. Inoltre, la presenza di programmi molto ingenui (come per esempio “Coopera sempre”) aveva dato un grosso vantaggio ai programmi più cattivi. Axelrod si rese conto che la vittoria di un programma sull’altro dipende molto dai programmi contro cui si scontra. Lavorando sulle combinazioni dei partecipanti al torneo scoprì che in certi casi persino il campione in carica Tit for tat veniva battuto.

I buoni vincono sempre
Lo scopo di Axelrod non era semplicemente divertirsi con il suo torneo. Il suo principale interesse era capire come in un gruppo di individui potesse sorgere l’istinto alla cooperazione. Sappiamo per certo che in natura la cooperazione esiste. Come fosse potuta nascere sulla base delle regole della selezione naturale darwiniana, però, era tutto un altro discorso. Se vi state domandando cosa diavolo hanno a che fare questi giochi da nerd con la realtà naturale, provate a fare questo esercizio. Immaginate che i vari programmi siano uccelli che abitano una colonia. Le “strategie” che praticano non sono altro che le istruzioni del loro codice genetico per risolvere un problema che sono costretti spesso ad affrontare. Questi uccelli, per esempio, sono infestati da un parassita che si attacca al collo, dove non possono raggiungerlo con il becco. Tra loro possono “cooperare”, strappandosi a vicenda i parassiti, oppure possono “tradire”, rifiutandosi di farlo. L’uccello che coopera e subisce un tradimento perde dei punti (ha sprecato tempo ed energie a spulciare l’altro senza ottenerne nulla) mentre l’altro ottiene il “punteggio” massimo. Se due uccelli cooperano ottengono un piccolo vantaggio (hanno sprecato tempo ed energie, ma almeno non hanno parassiti). Infine, se entrambi si ignorano subiscono un danno medio (non hanno perso tempo, ma ora sono infestati dai parassiti). La vittoria di Tit for tat sembrava fornire un’ottima spiegazione darwiniana al perché questi uccelli dovessero sviluppare un comportamento “cooperante”: semplicemente, è molto più conveniente che non farlo.

Come abbiamo visto, però, c’è un grosso problema. A seconda di chi sono i programmi che partecipano al torneo (o di che “tipi” sono gli uccelli che abitano la colonia), il comportamento cooperante rischia di non essere la strategia migliore. Per cercare di risolvere questo problema (che è davvero un problema: di fatto quasi tutte le specie in natura hanno tra loro una qualche forma di cooperazione e quindi è necessario spiegare come questo sia avvenuto), Axelrod fu aiutato dal biologo evoluzionista Richard Dawkins (che ha raccontato l’esperimento nel suo libro più noto, Il gene egoista). In una sorta di “terzo” torneo, Axelrod complicò ancora un po’ le regole. Alla fine di ogni girone i “punti” ottenuti si tramutavano in “figli”, cioè ulteriori copie dei vari uccelli/programmi. Chi faceva più punti diffondeva copie di sé stesso che si sarebbero affrontate nel girone successivo. Chi invece restava in fondo alla classifica si estingueva.

Variando la composizione iniziale delle strategie, Axelrod e Dawkins scoprirono che c’era una specie di “punto di rottura”. Se nella composizione iniziale della colonia c’erano troppi “cattivi” o troppi “ingenui totali” (individui che giocano sempre “cooperazione”, indipendentemente da cosa gioca il proprio avversario), Tit for tat era spacciato. Dopo un migliaio di generazioni la popolazione della colonia era composta soltanto da “cattivi” e tutti i buoni erano estinti. Con composizioni più equilibrate, invece, il trionfo di Tit for tat era assicurato. La poco consolante conclusione di questo esperimento era che l’altruismo è una buona strategia per un individuo soltanto se si trova in un ambiente adatto.

Ma Axelrod e Dawkins, a questo punto, fecero un passo indietro. D’accordo, in una popolazione con le giuste condizioni i cattivi possono vincere e l’istinto alla cooperazione può portare all’estinzione. Ma cosa accade quando mettiamo a confronto un gruppo dove hanno vinto i cattivi e uno dove hanno vinto i buoni? Immaginiamo due colonie di uccelli vicine (oppure immaginiamo che nella stessa colonia ci siano sotto-colonie che si incontrano più spesso tra di loro che non con il resto della colonia). In uno dei due gruppi i traditori finiscono con l’avere la meglio, nell’altra invece vincono i buoni. Pari e patta, quindi? Non proprio: i traditori, infatti, non hanno nessun vantaggio all’essere vicino ad altri traditori. Saranno sempre infestati da parassiti e quindi insalubri e malati (tradotto nelle regole del gioco: giocano sempre tradimento, quindi fanno pochi punti a ogni manche). L’altro gruppo, invece, è sano, e perfettamente privo di parassiti (giocano sempre cooperazione e guadagnano molti punti ad ogni round). Se questi due gruppi sono in competizione i cooperanti sfrutteranno il vantaggio di essere tutti insieme e, lentamente, porteranno all’estinzione i traditori. Rapaport, insomma, aveva ragione: alla fine, alla lunga, i buoni (e prudenti) vincono sempre.