Come fare gol su calcio d’angolo
Basta padroneggiare l'effetto Magnus, come spiegano Nicola Ludwig e Gianbruno Guerrerio nel loro libro La scienza nel pallone (essere Baggio o Roberto Carlos può essere d'aiuto)
di Gianbruno Guerrerio e Nicola Ludwig

Gennaio 2011: si gioca Corinthians–Portugesa, partita valevole per il campionato di calcio paulista. È il ventesimo del primo tempo: Roberto Carlos, monumento del calcio brasiliano, tornato a giocare in patria dopo molti anni di successi in Europa, si appresta a battere un calcio d’angolo alla destra della porta. Con i suoi 37 anni, di tiri dalla bandierina Roberto Carlos ne ha effettuati a centinaia nel corso della sua carriera. Questa volta però il tiro è speciale: vede che il portiere avversario è fuori dai pali, calcia di esterno sinistro e il pallone finisce in rete, fissando il punteggio sul 2 a 0 finale.
Il calcio dalla bandierina è un tiro sempre temibile, ma che la palla vada a insaccarsi direttamente in gol, senza che nessun giocatore intervenga per deviarne la traiettoria, sembrerebbe impossibile. Eppure, anche se di rado, qualche fuoriclasse riesce nell’impresa. Quando ciò accade, noi spettatori − come il portiere avversario − restiamo interdetti e sorpresi dalla traiettoria arcuata assunta dal pallone. Ci aspettiamo infatti che un oggetto, una volta scagliato, prosegua lungo la direzione di lancio, cambiando soltanto quota al passare del tempo, per via della forza di gravità Se invece un proiettile durante il volo si concede ripensamenti, deviazioni e cambiamenti di programma, come un qualsiasi turista in vacanza, la cosa ci appare quantomeno bizzarra. Nel calcio però questo «fuori programma» è talmente consueto e gradito che gli è stato dato anche un nome: lo si chiama effetto.
Tra i primi giocatori a padroneggiare con una certa sicurezza colpi che consentono alla palla di fare simili acrobazie molti ricordano ancora Mario Corso, ala sinistra dell’Inter degli anni Sessanta, non a caso soprannominato «il piede sinistro di Dio». Come ora vedremo, tuttavia, queste magie balistiche che sembrano sfidare le leggi della fisica hanno una spiegazione tutt’altro che trascendente.
La traiettoria: dall’intuizione alle leggi fisiche
Potrà sembrare strano, ma la comprensione delle leggi che governano il moto degli oggetti è molto recente nella storia dell’umanità: risale ad appena quattro secoli fa, allorché Galileo Galilei diede inizio agli studi sulla caduta dei gravi lasciando cadere una pietra dalla torre di Pisa.
Ci volle poi ancora quasi un secolo per arrivare alla teoria della gravitazione universale, alle leggi della dinamica di Newton e allo sviluppo del calcolo differenziale, indispensabile per le moderne definizioni di grandezze fisiche come la forza, la velocità, l’accelerazione e la quantità di moto. Prima dell’illustre pisano l’umanità aveva già lanciato ogni sorta di oggetto contro ogni essere del creato e contro i propri simili, con maggiore o minore efficacia, senza però elaborare un’adeguata teoria fisico-matematica che ne spiegasse il moto. Ciò non deve stupire, perché le leggi della fisica a volte sono anti intuitive, e per identificarle occorre un’attenta e paziente verifica sperimentale dei fenomeni naturali. Prima degli studi effettuati da Galileo, le conoscenze sul moto dei corpi erano riassunte nella teoria aristotelica dell’impetus. Elaborata compiutamente nel corso del Medioevo, la dottrina attribuiva il moto degli oggetti alla presenza continua di un «motore» invisibile capace di guidarli esercitando su di essi, per contatto, una forza. Omne quod movetur ab alio movetur, si diceva: tutto ciò che si muove è mosso da qualcosa.
Al di là della venerazione indiscussa che nel Medioevo si tributava alle dottrine aristoteliche, la teoria dell’impetus aveva successo perché era intuitiva. Oggi invece sappiamo che un oggetto può muoversi senza che gli sia applicata alcuna forza. Se l’oggetto si muove con velocità costante nel tempo, anzi, vuol proprio dire che la somma delle forze che agiscono su di esso è uguale a zero. Abbiamo anche capito che l’accelerazione che una data forza imprime a un oggetto dipende dalla massa dell’oggetto, e che la presenza di un fluido come l’aria o l’acqua si oppone sempre al moto. Inoltre sappiamo che la gittata di un lancio, ossia la distanza a cui un oggetto lanciato ricade al suolo, è determinata dalla velocità iniziale dell’oggetto, dalla forza di gravità e dalla resistenza dell’aria.
Grazie all’acquisizione di queste e altre conoscenze, nel corso degli ultimi secoli si è sviluppata una teoria del moto dei proiettili che formalizza in modo matematico la traiettoria seguita dagli oggetti in volo. Una traiettoria a cui in realtà siamo tutti abituati, visto che di solito riusciamo senza difficoltà ad afferrare un oggetto, quando qualcuno ce lo lancia. Tra i fenomeni legati al moto degli oggetti, tuttavia, alcuni ancora ci sorprendono e conservano qualcosa di magico. Il tiro a effetto nel calcio è uno di questi. Analoghe deviazioni dalla traiettoria «naturale» si verificano anche nel tennis, nel ping pong, nella pallavolo o nel golf, ma in nessuno di questi sport possono essere apprezzati altrettanto bene a occhio nudo come nel calcio. Proviamo a vedere allora che cos’è questo effetto e come «funziona» dal punta di vista fisico.
Punti, sfere e palloni da calcio
In cinematica, la parte della fisica che studia il movimento dei corpi, la traiettoria di un oggetto puntiforme in volo è determinata esclusivamente dalla sua velocità iniziale e dall’accelerazione di gravità a cui è sottoposto. Ciò fa sì che la traiettoria del corpo si sviluppi in un piano, cioè in due sole dimensioni: se appoggiassimo perpendicolarmente al suolo un foglio gigantesco, potremmo tracciare su di esso la traiettoria del proiettile puntiforme senza dover mai staccare la penna dal foglio. Ma sebbene sia utile per descrivere numerose situazioni reali, il concetto di «oggetto puntiforme» o «punto materiale» è soltanto un modello fisico idealizzato: si tratta cioè di una rappresentazione semplificata, che si può applicare quando l’oggetto considerato ha dimensioni trascurabili rispetto a quelle dell’ambiente in cui si muove.
Salvo che negli esercizi dei libri di fisica, però, noi non lanciamo punti materiali ma oggetti estesi, come un pallone da calcio, che hanno dimensioni confrontabili con il mondo circostante. In casi particolari, come per un lungo passaggio rasoterra calciato «di piatto», potremmo anche considerare il pallone come un punto materiale: la sua traiettoria infatti si può descrivere, in prima approssimazione, immaginando che tutta la massa sia concentrata nel baricentro (che coincide con il centro geometrico della sfera).
In generale però il pallone da calcio va considerato come un oggetto esteso, e ciò complica notevolmente lo studio del suo moto, perché obbliga a tener conto di fattori come la resistenza dell’aria o il fatto che il pallone, oltre a traslare, può anche ruotare. La resistenza dell’aria, o resistenza aerodinamica, è una forza di attrito: agisce lungo la stessa direttrice del moto ma in verso contrario, cioè si oppone sempre al movimento. Da secoli questa forza è studiata in relazione ai problemi di balistica, e quasi mai a scopo pacifico. La sua intensità varia con la forma dell’oggetto considerato e con la sua velocità durante il volo. La rotazione di un oggetto è lo spostamento angolare delle sue diverse parti rispetto a un punto dello spazio, o a una linea chiamata asse di rotazione. Una trottola per esempio ruota intorno a un asse di rotazione verticale; anche il nostro pianeta ha un asse di rotazione, e questa è la ragione per cui al giorno si alterna la notte.
Per far ruotare un oggetto occorre fornirgli energia. E se un oggetto ruota rapidamente su sé stesso mentre trasla, cioè si sposta, l’energia cinetica associata alla rotazione può essere paragonabile a quella di traslazione. Questo non è però il caso dei palloni da calcio, perché le velocità di rotazione che si osservano in campo sono relativamente basse [Un calciatore molto abile può calciare il pallone a 25 m/s facendolo ruotare su sé stesso 5 volte al secondo (cioè con una frequenza di 5 hertz). In tal caso la velocità tangenziale di un punto all’«equatore» sulla superficie del pallone (che ha raggio di 11 cm circa) raggiunge il valore 2π·(0,11 m)·(5 Hz) = 3,5 m/s, ossia soltanto il 14% della velocità di traslazione del pallone]. Inoltre la rotazione, una volta attivata, può permanere a lungo. Una trottola può continuare a ruotare anche per più di un minuto, finché la sua energia cinetica di rotazione non è dissipata per attrito con l’aria che la circonda.
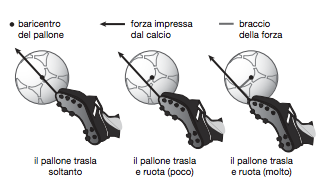
Figura 8. Con un calcio si applica a un pallone una certa forza. Quanto maggiore è il braccio della forza rispetto al baricentro del pallone, tanto maggiore sarà la velocità con cui esso ruoterà su sé stesso durante il volo.
Quando la palla fa la trottola
Come si fa a trasformare un pallone da calcio in una trottola? Per capirlo bisogna tenere presente il fatto che, quando si applica a un oggetto una forza esterna, il moto che ne risulta dipende dal punto di applicazione della forza. Se si applica una forza la cui direzione passa per il centro di massa del corpo, essa si distribuisce in egual misura fra tutti i punti dell’oggetto e ne provoca una semplice traslazione (come a sinistra nella figura 8). Se invece la direzione della forza applicata non passa per il centro di massa, le diverse parti dell’oggetto risentono in maniera diversa della sua azione, e di conseguenza l’oggetto oltre a traslare si mette a ruotare (come nei disegni di destra della figura 8).
La velocità della rotazione che si riesce a imprimere dunque non dipende soltanto dall’intensità della forza applicata, ma anche dalla distanza fra la direzione della forza e il baricentro dell’oggetto; questa distanza, evidenziata nella figura 8, si chiama braccio della forza. Dal punto di vista fisico la grandezza effettivamente responsabile della rotazione dei corpi è il momento della forza, che si ottiene moltiplicando l’intensità della forza applicata per la lunghezza del suo braccio.
Se colpiamo il pallone esattamente «in mezzo», se cioè il centro della sfera è allineato con la direzione in cui vogliamo calciarlo, esso traslerà senza ruotare su sé stesso. Se invece vogliamo metterlo in rotazione, dovremo calciarlo un po’ «di lato», per fare in modo che il braccio della forza che imprimiamo sia diverso da zero. L’asse intorno a cui ruoterà il pallone sarà la retta che passa per il baricentro del pallone ed è perpendicolare al piano su cui giacciono la forza e il braccio.
Bene, un pallone in volo generalmente possiede entrambi i moti, traslatorio e rotatorio. La componente traslatoria in prima approssimazione può essere trattata come per un punto materiale posto nel centro della sfera, purché si tenga conto anche della resistenza dell’aria. La componente rotatoria invece introduce qualcosa di veramente inatteso: finisce infatti per influire proprio sulla direzione del moto traslatorio, facendo sì che esso non si svolga più all’interno di un piano verticale, ma abbia una traiettoria tridimensionale. Infatti l’«effetto» di un tiro, come vedremo, è determinato proprio dal fatto che il pallone è un oggetto esteso che ruota in presenza della resistenza dell’aria.
La resistenza aerodinamica
Un pallone in movimento, che ruoti o meno, deve sempre fare i conti con l’aria che lo circonda. Che cosa succede quando il pallone si muove attraverso una massa d’aria? Per capirlo dobbiamo ricorrere a una legge fondamentale nota come teorema di Bernoulli, dal nome del fisico svizzero che la enunciò nel Settecento. Questa legge non è altro che il principio di conservazione dell’energia applicato ai cosiddetti flussi stazionari di fluidi come l’acqua quando scorre in un tubo, o l’aria di un vento costante. L’aggettivo «stazionario» indica che la velocità del fluido, anche se da punto a punto può variare, in ogni data posizione rimane invece sempre la stessa al passare del tempo. Il teorema di Bernoulli afferma che esiste una quantità che non cambia nel tempo: è la somma della pressione del fluido, della sua energia cinetica e della sua energia potenziale (legata alla quota a cui si trova) [Si sta parlando, per essere precisi, di densità di energia, cioè di energia per unità di volume del fluido considerato]. Per i nostri scopi, se pensiamo a tiri in cui il pallone viaggia al massimo pochi metri al di sopra del terreno di gioco, possiamo trascurare le variazioni di energia potenziale dell’aria. La legge di Bernoulli ha allora la forma matematica: p + ½ d·v2= costante; p è la pressione dell’aria e v
è la velocità con cui scorre attorno al pallone.
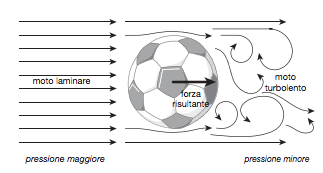
Figura 9. Il flusso di aria laminare proveniente da sinistra incontra la palla. A destra della sfera si generano vortici, il flusso diviene turbolento e la velocità dell’aria aumenta. Si genera così una differenza di pressione e sulla palla si esercita una spinta verso destra: è la resistenza aerodinamica
Per il principio di relatività dei moti, naturalmente, v è anche la velocità del pallone attraverso l’aria. Ragioneremo, in altre parole, mettendoci dal punto di vista del pallone: esso è fermo e vede arrivare contro di sé un flusso d’aria con velocità v [Questa è proprio la situazione che si verifica nelle gallerie del vento, quando si eseguono prove di aerodinamicità per oggetti di ogni tipo, dalle automobili ai palloni da calcio: un forte flusso d’aria viene indirizzato contro l’oggetto fermo.] Nella formula d è la densità dell’aria, pari a circa 1 kg per metro cubo, che si può considerare costante nelle situazioni di cui ci occuperemo. Nel nostro caso, dunque, il fatto che al secondo membro nella legge di Bernoulli ci sia un valore costante implica che, se la pressione p diminuisce, la velocità v dovrà aumentare, e viceversa. La figura 9 mostra che cosa accade quando un flusso d’aria incontra un pallone. Il pallone è fermo mentre il flusso d’aria si muove da sinistra verso destra (una situazione, come già detto, equivalente a quella in cui il pallone avanza da destra verso sinistra nell’aria ferma). Prima di incontrare la palla, il flusso d’aria si muove ordinatamente e con una certa velocità iniziale (moto laminare del fluido).
A causa della forma sferica dell’ostacolo, dietro al pallone si creano vortici: qui l’aria si muove in modo disordinato e la sua velocità aumenta (moto turbolento del fluido).
Sebbene il flusso ora non sia stazionario, perché nella «scia» dell’ostacolo la velocità locale cambia da un istante all’altro, la relazione qualitativa tra velocità e pressione continua a essere quella prevista dalla legge di Bernoulli: l’aumento della velocità dell’aria a valle del pallone è accompagnato da una diminuzione della sua pressione. Sui due lati della palla si ha così una differenza di pressione, e questa produce una forza che spinge il pallone nella direzione e nel verso della velocità del flusso d’aria; la sua intensità, per una data velocità, dipende dalla forma dell’ostacolo.
Quando si cambia il punto di vista − o, come dicono i fisici, il sistema di riferimento − ed è il pallone a muoversi nell’aria ferma, questa forza è la resistenza dell’aria. Il pallone da calcio è un esempio di ciò che i fisici chiamano corpo tozzo: la forma sferica è molto efficace nel creare vortici, perciò risente di una forte resistenza quando si muove nell’aria. L’opposto vale per gli oggetti con forma aerodinamica, come automobili e aerei, progettati in modo da far sì che l’aria scorra attorno a loro con perturbazione ridotta al minimo. In molti sport si cerca di limitare l’effetto frenante della resistenza dell’aria. Per esempio la butteratura delle palline da golf serve proprio per generare vortici anche davanti alla palla, oltre che nella scia, riducendo così la resistenza aerodinamica.
L’effetto della resistenza sulla traiettoria dei tiri
Nel corso della traiettoria di un tiro, l’angolo tra la forza di gravità e la forza di resistenza dell’aria cambia continuamente. L’abbiamo visto nella figura 6 del capitolo 2, che è riprodotta qui mostrando soltanto la forza di gravità e la resistenza dell’aria. Il disegno può schematizzare per esempio il rinvio di un portiere da sinistra verso destra.
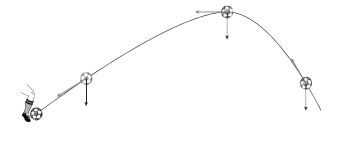
Nella parte ascendente della traiettoria la resistenza è rivolta verso il basso, nel punto più alto per un istante è parallela al suolo, poi nella parte discendente è rivolta verso l’alto. All’inizio dunque la resistenza dell’aria ha una componente verticale diretta verso il basso, cioè «appesantisce» la palla, mentre nella parte finale della traiettoria una parte di questa forza è diretta verso l’alto, si oppone alla gravità, e quindi «alleggerisce» la palla. Dunque la risultante delle forze che agisce su un pallone in volo non ha una direzione costante, e ciò trasforma la traiettoria del pallone da parabolica (come sarebbe in presenza della sola gravità) ad «allungata in avanti», come si vedeva bene nella figura 6.
Osserviamo infine che l’intensità della resistenza aerodinamica di cui risente un oggetto sferico dipende in modo tutt’altro che banale dalla sua velocità, come mostra il grafico della figura 10. La resistenza aumenta fino a un valore critico della velocità, poi diminuisce bruscamente; infine, dopo aver raggiunto un valore minimo, riprende ad aumentare. Questo andamento molto particolare è dovuto al fatto che l’aria attorno al pallone fluisce in modo più o meno turbolento proprio al variare della velocità.
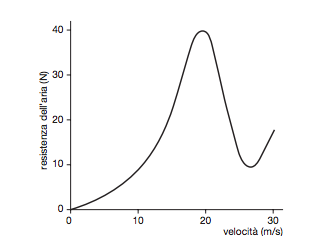
Figura 10. La resistenza aerodinamica in funzione della velocità per una sfera perfettamente liscia (da Physics World Magazine, IOP giugno 1998).
Il grafico della figura 10 si riferisce a un pallone da calcio «ideale», una sfera perfettamente liscia: in tal caso il flusso d’aria si trasforma da molto turbolento (più resistente) a poco turbolento (meno resistente) a una velocità critica vicina a 20 m/s, circa 70 km/h. Se prendessimo alla lettera il grafico della figura 10, dovremmo aspettarci che un tiro molto forte incontri nell’aria resistenza minore rispetto a un tiro di media velocità.
Questo fenomeno davvero sorprendente tuttavia non si manifesta in maniera così evidente, perché i palloni da calcio non sono sfere ideali: la presenza delle cuciture sulla superficie modifica la curva della figura 10, rendendola molto meno accentuata e spostando la velocità critica, che si riduce a circa 10 m/s, cioè 36 km/h, un valore inferiore alle velocità tipiche dei tiri in campo.
L’effetto Magnus
In un torneo di calcio interplanetario giocato sulla Luna, un giocatore che tira una punizione non riuscirebbe mai ad aggirare la barriera. Certo, potrebbe calciare la palla in modo da farla ruotare su sé stessa, ma questo non basterebbe per produrre una traiettoria a effetto. Sulla Luna manca infatti un ingrediente fondamentale dei tiri «a girare»: l’aria. In questo e nel prossimo paragrafo vedremo invece che cosa succede, qui sulla Terra, quando un pallone ruota su sé stesso e vola non nel vuoto, ma attraverso l’aria. In ambito sportivo il primo a ragionare in modo sistematico sulle conseguenze della rotazione di una palla per la sua traiettoria è stato, a fine Ottocento, il matematico scozzese Peter Tait.
Come molti suoi connazionali, tuttavia, Tait era un appassionato giocatore di golf e l’oggetto dei suoi studi non furono palloni di cuoio, ma palline bianche da mettere in buca. Per calcolare la gittata di un drive, si domandava Tait, basta tenere conto della forza di gravità oppure bisogna considerare anche la resistenza dell’aria? Provando a fare i conti, notò qualcosa di sorprendente: se considerava soltanto la gravità agente sulla pallina, il calcolo della gittata sottostimava l’effettiva lunghezza dei colpi; ma se aggiungeva anche la resistenza aerodinamica dell’aria, allora il risultato sovrastimava la lunghezza del tiro.
Qualcosa evidentemente gli stava sfuggendo: era come se sulla pallina agisse una forza capace di farla «galleggiare» e al tempo stesso di rallentarla durante il volo. Quale poteva essere l’origine di questa forza?
Lo scienziato scozzese notò che quando la pallina era colpita in modo da metterla in rotazione retrograda, la gittata era più lunga. Quando invece la rotazione avveniva in avanti, cioè la pallina «rotolava» nel senso del moto durante il volo, allora la gittata era più breve. Forse Tait era a conoscenza di una comunicazione del 1671 alla Royal Society in cui niente meno che Isaac Newton aveva riferito un’osservazione simile. Newton scrisse di essere stato ispirato, nell’elaborazione della sua teoria dei colori, dall’osservazione che una palla da tennis devia dalla traiettoria attesa quando viene colpita «di taglio» con la racchetta. Il padre della fisica moderna aveva tuttavia interpretato il fenomeno in modo errato, associandolo a un effetto di deviazione ottico simile a quello che la luce subisce attraversando un prisma.
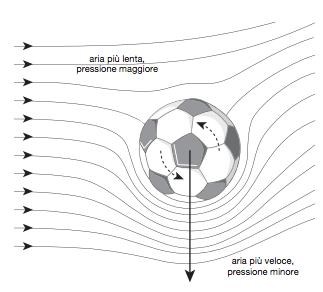
Figura 11a. Una sfera che ruota su sé stessa si muove nell’aria da destra verso sinistra. Qui la rotazione è retrograda; la freccia verticale rappresenta la portanza generata.
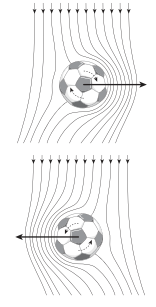
La questione dell’«effetto» non fu risolta da Tait ma dal fisico tedesco Heinrich Gustav Magnus, al cui nome il fenomeno è poi rimasto indissolubilmente legato. Nella seconda metà dell’Ottocento Magnus scoprì la spiegazione dopo un attento studio sperimentale del comportamento di un cilindro rotante sospeso all’interno di una corrente fluida; facendo ruotare il cilindro attorno al proprio asse, si osserva una forza che lo spinge verso l’alto oppure verso il basso, a seconda del verso di rotazione. Come già accennato, le condizioni necessarie perché nel calcio si verifichi il fenomeno che ci interessa sono due: la rotazione della palla in volo e la presenza dell’aria. Esaminiamo ora la figura 11a, immaginando che rappresenti la sfera vista di lato mentre avanza veloce nell’aria da destra verso sinistra, con rotazione retrograda e asse di rotazione parallelo al suolo.
In alto, dove la superficie della sfera e l’aria «corrono» nello stesso verso, il fluido viene accelerato dalla rotazione della superficie. In basso avviene invece l’opposto: il flusso d’aria e la superficie della palla si muovono in verso opposto, di conseguenza la velocità dell’aria diminuisce.
Questa differenza di velocità tra il fluido ai lati opposti della sfera genera − per la legge di Bernoulli− una differenza di pressione: la pressione del fluido in basso è maggiore di quella in alto, perciò sulla sfera agisce una forza perpendicolare alla direzione del moto e diretta verso l’alto. È proprio questa la forza che fa «galleggiare» in aria una pallina da golf colpita da sotto (così che ruoti in modo retrogrado). Si tratta di un esempio di portanza, la stessa forza che fa decollare un aereo e spinge le barche a vela. Lo stesso effetto è sfruttato nel tennis e nel ping pong per le smorzate, e nel calcio per prolungare la gittata dei rilanci dal fondo, dei cross dalle fasce o dei pallonetti (come il cosiddetto «cucchiaio» reso celebre da Francesco Totti).
Per la figura 11b, dove la sfera ruota «in avanti», vale un discorso del tutto simile, ma le conseguenze sono diametralmente opposte. In questo caso il fluido rallenta in alto e accelera in basso, con il risultato che la differenza di pressione genera una «portanza negativa», diretta cioè verso il basso. È quello che succede nel caso del top spin, con cui nel tennis e nel ping pong si «chiude» verso il basso la traiettoria della palla; la stessa tecnica si usa anche nella pallavolo per le schiacciate o le battute alte in salto.
Nel calcio una punizione tirata facendo ruotare il pallone in avanti può sorprendere il portiere, perché la discesa del pallone è più rapida di quanto ci si aspetterebbe in base alla sola forza di gravità (figura 12).
Questo effetto, che già cinquant’anni fa era usato nella «foglia morta» di Didì (il brasiliano Valdir Pereira) e Mariolino Corso, oggi fa parte del repertorio di campioni come Andrea Pirlo e Juninho. L’efficacia del tiro aumenta se verso la fine del volo la palla è così rallentata da avvicinarsi alla velocità critica alla quale la resistenza aerodinamica diventa massima, come abbiamo visto nella figura 10.
Se il tiro è piuttosto lento fin dall’inizio, il pallone può raggiungere la velocità critica in prossimità dell’apice della traiettoria. In questo caso eccezionale si ha un’improvvisa frenata in aria, la palla oscilla, ondeggia e cade come foglia morta cade. Dunque sia il «colpo da sotto» o backspin (con rotazione retrograda) sia il top spin (con rotazione della palla in avanti) sfruttano l’effetto Magnus. Questo effetto si manifesta quando il pallone ruota su sé stesso in aria e produce una spinta che è perpendicolare all’asse di rotazione e alla direzione di moto, e dunque non è necessariamente verticale.
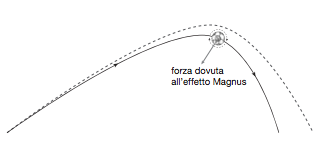
Figura 12. L’azione frenante della forza dovuta all’effetto Magnus nella traiettoria di un pallone che ruota in avanti.
Il tiro a effetto laterale
Quando nel calcio si parla di effetto, la mente degli appassionati vola subito al magico tiro «a rientrare», che negli Stati Uniti con efficace metafora chiamano banana kick. Il segreto di questo colpo spettacolare? È di nuovo l’effetto Magnus. Per capirlo basta riguardare le figure 11a e 11b ma, questa volta, immaginando che il moto della sfera sia osservato non di lato ma dall’alto, come con una telecamera posta sopra il terreno di gioco e puntata verso il basso.
Ora l’asse di rotazione della sfera è dunque perpendicolare al terreno di gioco, e le zone superiore e inferiore dei disegni rappresentano, dal punto di vista dei calciatori, la destra e la sinistra.
Se il pallone visto dall’alto ruota in verso antiorario, come nella figura 11a, durante il volo riceverà per effetto Magnus una spinta verso destra. Se invece il pallone ruota in verso opposto, come nella figura 11b, riceverà una spinta verso sinistra. In entrambi i casi si ha dunque una forza simile alla portanza, che ora però agisce lateralmente sul pallone. Essa fa curvare la traiettoria senza influire significativamente sul tempo di volo e sulla gittata del tiro (che continuano a essere determinate dalla forza di gravità e dalla resistenza dell’aria).
L’effetto è sorprendente perché il moto non avviene più all’interno di un piano: nel caso di un calcio di punizione, per esempio, il pallone all’inizio segue una normale traiettoria rettilinea, ma poi progressivamente curva sotto la spinta laterale della portanza, consentendo di aggirare la barriera anche quando essa copre la visuale della porta. Il calcio di punizione forse più leggendario nella storia del calcio è stato tirato il 3 giugno 1997 da Roberto Carlos − l’«artista dell’effetto» autore anche del calcio d’angolo citato a inizio capitolo − in un incontro tra Brasile e Francia valevole per la Confederations Cup (figura 13). Dopo una lunga rincorsa, Roberto Carlos calciò da circa 30 metri di esterno sinistro, imprimendo così al pallone una forte rotazione in senso antiorario (se vista dall’alto).
La palla, prima di insaccarsi in rete colpendo l’interno del palo alla sinistra del portiere, deviò dalla sua ipotetica traiettoria rettilinea iniziale addirittura di quasi 6 metri! Un giocatore che usa il piede destro otterrà lo stesso tipo di effetto colpendo la palla con l’interno del piede, come nei tiri che per anni hanno costituito il «marchio di fabbrica» di Alessandro Del Piero. Se invece si calcia con l’esterno del piede destro, la palla girerà verso destra e in una punizione si potrà aggirare la barriera dal lato opposto rispetto al caso della figura 13. Nella realtà un tiro a effetto contiene sempre entrambe le componenti, di spinta verticale e laterale, non tanto perché sia difficile imprimere al pallone una rotazione perfettamente verticale od orizzontale (i grandi campioni ci riescono senza problemi), ma perché l’effetto complessivo di curvatura per aggirare la barriera deve essere reso imprevedibile.
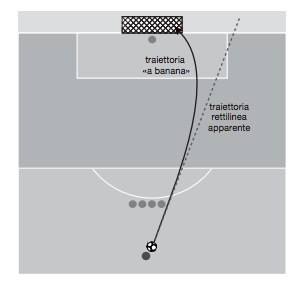
Figura 13. La traiettoria della straordinaria punizione di Roberto Carlos in Brasile-Francia del 1997.
Ciò che fa la differenza e può portare al gol è – come sempre quando si affrontano campioni di eguale e straordinaria preparazione atletica – il fattore sorpresa: la capacità di realizzare traiettorie non intuibili dall’avversario.
È l’effetto Magnus che dà la possibilità ai più grandi campioni di inventare azioni del tutto sorprendenti, che rendono più spettacolare il gioco del calcio.
È uscito per Zanichelli La scienza nel pallone, di Nicola Ludwig e Gianbruno Guerrerio. Nicola Ludwig è ricercatore all’Università Statale di Milano e autore di spettacoli di teatro-scienza per ragazzi. Gianbruno Guerrerio, giornalista scientifico, cura il notiziario quotidiano online della rivista Le Scienze ed è autore di una biografia scientifica del logico e matematico Kurt Gödel.






